题目内容
、设函数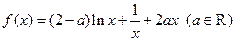 .
.
(Ⅰ)当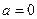 时,求
时,求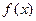 的极值;
的极值;
(Ⅱ)当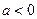 时,求
时,求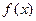 的单调区间;
的单调区间;
(Ⅲ)若对任意 及
及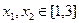 ,恒有
,恒有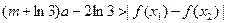
成立,求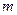 的取值范围.
的取值范围.
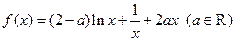 .
.(Ⅰ)当
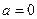 时,求
时,求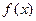 的极值;
的极值;(Ⅱ)当
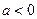 时,求
时,求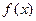 的单调区间;
的单调区间;(Ⅲ)若对任意
 及
及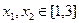 ,恒有
,恒有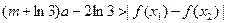
成立,求
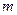 的取值范围.
的取值范围.解:(Ⅰ)依题意,知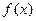 的定义域为
的定义域为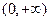 .
.
当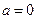 时,
时,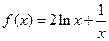 ,
,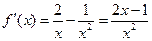 .
.
令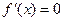 ,解得
,解得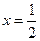 .……2分
.……2分
当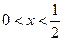 时,
时,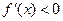 ;当
;当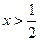 时,
时,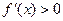 .
.
又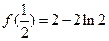 ,所以
,所以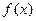 的极小值为
的极小值为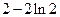 ,无极大值 .………4分
,无极大值 .………4分
(Ⅱ)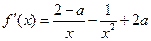
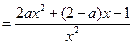 …………5分
…………5分
当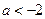 时,
时,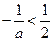 , 令
, 令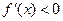 ,得
,得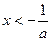 或
或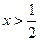 ,令
,令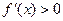 ,
,
得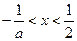 ;…………6分,当
;…………6分,当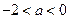 时,得
时,得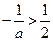 ,令
,令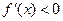 ,得
,得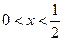 或
或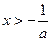 ,令
,令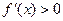 ,得
,得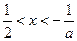 ;当
;当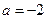 时,
时,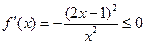 .8分
.8分
综上所述,当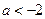 时,
时,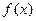 的递减区间为
的递减区间为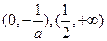 ;递增区间为
;递增区间为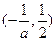 .
.
当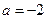 时,
时,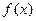 在
在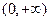 单调递减.
单调递减.
当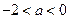 时,
时,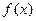 的递减区间为
的递减区间为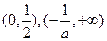 ;递增区间为
;递增区间为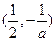 .…(9分)
.…(9分)
(Ⅲ)由(Ⅱ)可知,当 时,
时,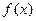 在
在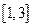 单调递减.
单调递减.
当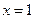 时,
时,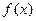 取最大值;当
取最大值;当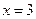 时,
时,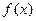 取最小值.
取最小值.
所以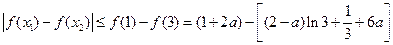
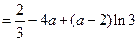 .……11分
.……11分
因为 恒成立,
恒成立,
所以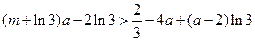 ,整理得
,整理得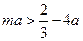 .
.
又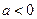 所以
所以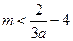 , 又因为
, 又因为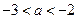 ,得
,得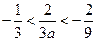 ,
,
所以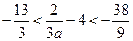 所以
所以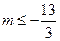 .………14分
.………14分
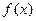 的定义域为
的定义域为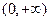 .
.当
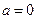 时,
时,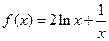 ,
,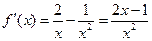 .
.令
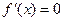 ,解得
,解得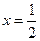 .……2分
.……2分当
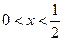 时,
时,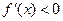 ;当
;当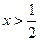 时,
时,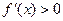 .
.又
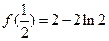 ,所以
,所以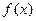 的极小值为
的极小值为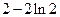 ,无极大值 .………4分
,无极大值 .………4分(Ⅱ)
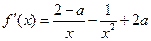
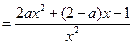 …………5分
…………5分当
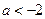 时,
时,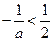 , 令
, 令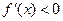 ,得
,得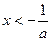 或
或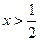 ,令
,令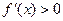 ,
,得
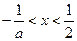 ;…………6分,当
;…………6分,当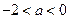 时,得
时,得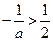 ,令
,令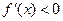 ,得
,得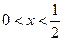 或
或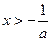 ,令
,令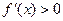 ,得
,得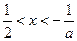 ;当
;当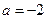 时,
时,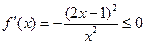 .8分
.8分综上所述,当
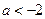 时,
时,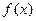 的递减区间为
的递减区间为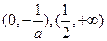 ;递增区间为
;递增区间为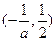 .
.当
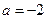 时,
时,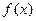 在
在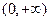 单调递减.
单调递减.当
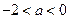 时,
时,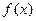 的递减区间为
的递减区间为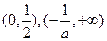 ;递增区间为
;递增区间为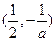 .…(9分)
.…(9分)(Ⅲ)由(Ⅱ)可知,当
 时,
时,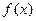 在
在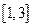 单调递减.
单调递减.当
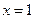 时,
时,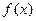 取最大值;当
取最大值;当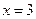 时,
时,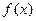 取最小值.
取最小值.所以
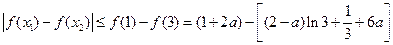
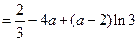 .……11分
.……11分因为
 恒成立,
恒成立,所以
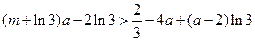 ,整理得
,整理得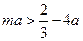 .
.又
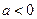 所以
所以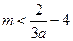 , 又因为
, 又因为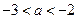 ,得
,得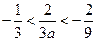 ,
,所以
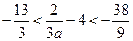 所以
所以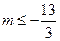 .………14分
.………14分略

练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目
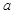 为实数,函数
为实数,函数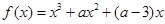 的导函数为
的导函数为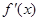 ,且
,且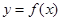 在原点处的切线方程为( )
在原点处的切线方程为( )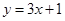
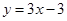
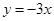
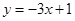
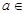 R,函数
R,函数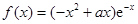 .(
.( R,e为自然对数的底数)
R,e为自然对数的底数)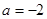 时,求函数
时,求函数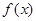 的单调递减区间;
的单调递减区间;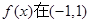 内单调递减,求a的取值范围;
内单调递减,求a的取值范围;
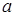 为实数,函数
为实数,函数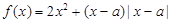 .
.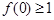 ,求
,求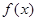 的最小值.
的最小值.
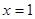 处的切线方程为12x+y-1=0.
处的切线方程为12x+y-1=0.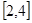 上的最大值和最小值.
上的最大值和最小值.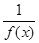 ,又当-3≤x≤-2时,f(x)=2x,则f(113.5)的值是( )
,又当-3≤x≤-2时,f(x)=2x,则f(113.5)的值是( )

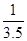
 1处取得极值
1处取得极值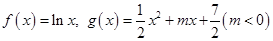 ,直线
,直线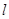 与函数
与函数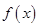 、
、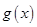 的图象都相切,且与函数
的图象都相切,且与函数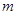 的值为___________。
的值为___________。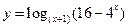 的定义域.
的定义域.