题目内容
已知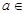 R,函数
R,函数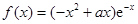 .(
.( R,e为自然对数的底数)
R,e为自然对数的底数)
(Ⅰ)当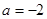 时,求函数
时,求函数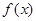 的单调递减区间;
的单调递减区间;
(Ⅱ)若函数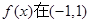 内单调递减,求a的取值范围;
内单调递减,求a的取值范围;
(Ⅲ)函数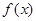 是否为R上的单调函数,若是,求出a的取值范围;若不是,请说明理由.
是否为R上的单调函数,若是,求出a的取值范围;若不是,请说明理由.
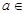 R,函数
R,函数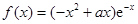 .(
.( R,e为自然对数的底数)
R,e为自然对数的底数)(Ⅰ)当
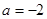 时,求函数
时,求函数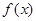 的单调递减区间;
的单调递减区间;(Ⅱ)若函数
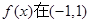 内单调递减,求a的取值范围;
内单调递减,求a的取值范围;(Ⅲ)函数
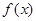 是否为R上的单调函数,若是,求出a的取值范围;若不是,请说明理由.
是否为R上的单调函数,若是,求出a的取值范围;若不是,请说明理由.
(Ⅰ)当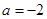 时,
时,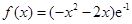
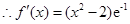 ……………………………………………………………………1分
……………………………………………………………………1分
令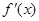
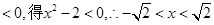 ……………………………………………2分
……………………………………………2分
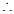
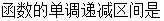 (-
(-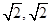 ).
).
(注:写成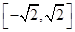 也对) ………………………………………………………3分
也对) ………………………………………………………3分
(Ⅱ)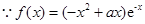
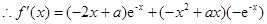
=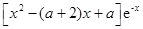 . ………………………………………………………………4分
. ………………………………………………………………4分
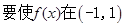 上单调递减,
上单调递减,
则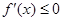 对
对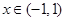 都成立,
都成立,
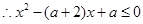 对
对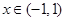 都成立.…………………………………………5分
都成立.…………………………………………5分
令 ,则
,则
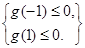 …………………………………………………………………………7分
…………………………………………………………………………7分
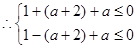
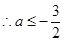 .
. (注:不带等号扣1分) ………………………………………………8分
(注:不带等号扣1分) ………………………………………………8分
(Ⅲ)①若函数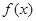 在R上单调递减,则
在R上单调递减,则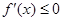 对
对 R 都成立
R 都成立
即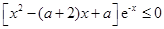 对
对 R都成立.…………………………………………9分
R都成立.…………………………………………9分
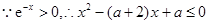 对
对 R都成立
R都成立
令 ,
,
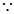 图象开口向上
图象开口向上 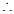 不可能对
不可能对 R都成立
R都成立
②若函数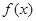 在R上单调递减,则
在R上单调递减,则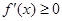 对
对 R都成立,
R都成立,
即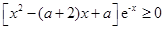 对
对 R都成立,
R都成立,
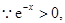
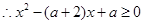 对
对 R都成立.
R都成立.
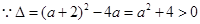
故函数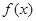 不可能在R上单调递增.
不可能在R上单调递增.
综上可知,函数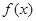 不可能是R上的单调函数
不可能是R上的单调函数
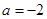 时,
时,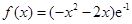
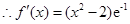 ……………………………………………………………………1分
……………………………………………………………………1分令
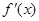
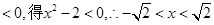 ……………………………………………2分
……………………………………………2分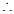
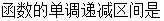 (-
(-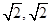 ).
).(注:写成
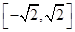 也对) ………………………………………………………3分
也对) ………………………………………………………3分(Ⅱ)
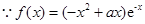
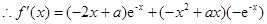
=
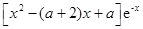 . ………………………………………………………………4分
. ………………………………………………………………4分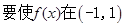 上单调递减,
上单调递减,则
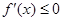 对
对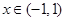 都成立,
都成立,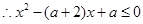 对
对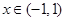 都成立.…………………………………………5分
都成立.…………………………………………5分令
 ,则
,则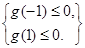 …………………………………………………………………………7分
…………………………………………………………………………7分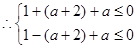
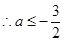 .
. (注:不带等号扣1分) ………………………………………………8分
(注:不带等号扣1分) ………………………………………………8分(Ⅲ)①若函数
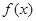 在R上单调递减,则
在R上单调递减,则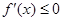 对
对 R 都成立
R 都成立即
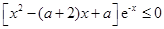 对
对 R都成立.…………………………………………9分
R都成立.…………………………………………9分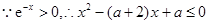 对
对 R都成立
R都成立令
 ,
,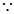 图象开口向上
图象开口向上 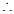 不可能对
不可能对 R都成立
R都成立 ②若函数
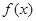 在R上单调递减,则
在R上单调递减,则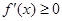 对
对 R都成立,
R都成立,即
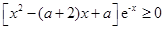 对
对 R都成立,
R都成立,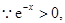
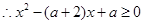 对
对 R都成立.
R都成立.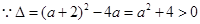
故函数
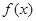 不可能在R上单调递增.
不可能在R上单调递增.综上可知,函数
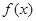 不可能是R上的单调函数
不可能是R上的单调函数略

练习册系列答案
相关题目
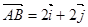 (
(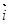 、
、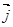 分别是与x、y轴正半轴同方向的单位向量), 函数g(x)=x2-x-6.
分别是与x、y轴正半轴同方向的单位向量), 函数g(x)=x2-x-6. 的最小值.
的最小值.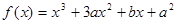 在
在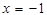 时有极值0.
时有极值0.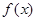 的单调区间.
的单调区间.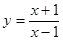 在点(3,2)处的切线与直线
在点(3,2)处的切线与直线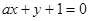 垂直,则
垂直,则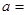
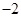
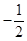
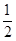
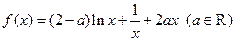 .
.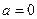 时,求
时,求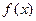 的极值;
的极值;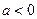 时,求
时,求 及
及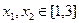 ,恒有
,恒有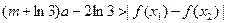
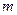 的取值范围.
的取值范围.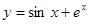 在点
在点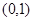 处的切线方程是
处的切线方程是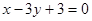
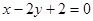
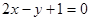

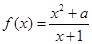 在
在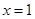 处取极值,则
处取极值,则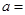
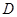 上的函数
上的函数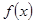 对
对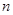 个值
个值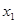 ,
,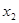 ,…,
,…,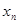 ,总满足
,总满足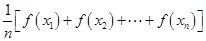 ≤
≤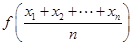 ,则称
,则称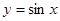 在区间
在区间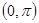 上是“凸函数”,则在
上是“凸函数”,则在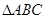 中,
中,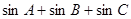 的最大值是___________
的最大值是___________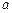 、
、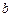 万元,则农民购买家电产品获得的补贴分别为
万元,则农民购买家电产品获得的补贴分别为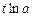 万元、
万元、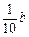 万元(
万元(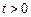 且为常数).已知该企业投放总价值为100万元的A、B两种型号的家电产品,且A、B两种型号的投放金额都不低于10万元.
且为常数).已知该企业投放总价值为100万元的A、B两种型号的家电产品,且A、B两种型号的投放金额都不低于10万元.