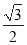题目内容
已知函数f(x)=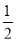 (x2+a)的图象在点Pn(n,f(n))(n∈N*)处的切线ln的斜率为kn,直线ln交x轴,y轴分别于点An(xn,0),Bn(0,yn),且y1=-1.给出以下结论:
(x2+a)的图象在点Pn(n,f(n))(n∈N*)处的切线ln的斜率为kn,直线ln交x轴,y轴分别于点An(xn,0),Bn(0,yn),且y1=-1.给出以下结论:
①a=-1;
②记函数g(n)=xn(n∈N*),则函数g(n)的单调性是先减后增,且最小值为 ;
;
③当n∈N*时, ;
;
④当n∈N*时,记数列 的前
的前 项和为
项和为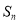 ,则
,则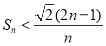 .
.
其中,正确的结论有 (写出所有正确结论的序号)
①③④
【解析】由已知,f '(x)=x,于是kn=n,且f(n)= (n2+a),
(n2+a),
所以ln:y- (n2+a)=n(x-n)
(n2+a)=n(x-n)
①在ln中,令n=1,x=0,y=-1,得a=-1,故①正确;
且有ln:y- (n2-1)=n(x-n)
(n2-1)=n(x-n)
②在ln中,令y=0,得xn=- (n-
(n- )+n=
)+n= (n+
(n+ )
)
n∈N*时,该函数为增函数,没有递减部分,故②错误;
③在ln中,令x=0,得yn=-n2+ (n2-1)=-
(n2-1)=- (n2+1)
(n2+1)
∴yn+kn+ =-
=- n2+n
n2+n
当n=1时,y1+k1+ =
= =ln
=ln <ln2=ln(1+1)=ln(1+k1)
<ln2=ln(1+1)=ln(1+k1)
当n≥2时,yn+kn+ =-
=- n2+n≤0,而ln(1+kn)=ln(1+n)>ln1=0,故③正确
n2+n≤0,而ln(1+kn)=ln(1+n)>ln1=0,故③正确
 ,
,
∴Sn<
当n>1时,
∴Sn<
= ,故④正确.
,故④正确.
考点:函数、导数、数列、不等式等综合应用

练习册系列答案
 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案
相关题目
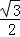 B.
B.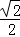 C.
C.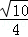 D.
D.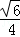
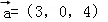 同向共线的单位向量
同向共线的单位向量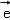 为( )
为( )
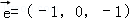
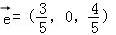
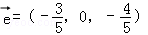
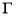 :
: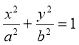 (
( )的右焦点为
)的右焦点为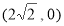 ,且过点
,且过点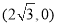 .
. 与椭圆
与椭圆 交于不同两点
交于不同两点 、
、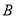 ,且
,且 .若点
.若点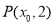 满足
满足 ,求
,求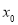 的值.
的值.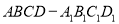 棱长为4,点
棱长为4,点 在棱
在棱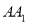 上,且
上,且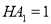 .点
.点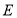 ,
,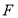 分别为棱
分别为棱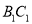 ,
,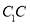 的中点,
的中点,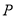 是侧面
是侧面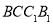 内一动点,且满足
内一动点,且满足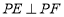 .则当点
.则当点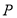 运动时,
运动时,  的最小值是
的最小值是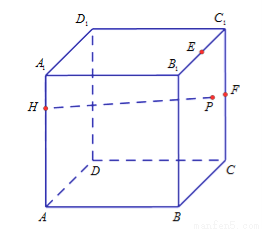
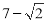 (B)
(B)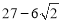
 (D)
(D)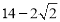
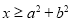 ,则
,则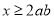 ”的逆命题是
”的逆命题是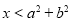 ,则
,则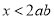
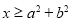 ,则
,则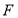 是椭圆
是椭圆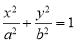 (
(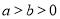 )的左焦点,
)的左焦点,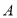 为右顶点,
为右顶点,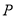 是椭圆上一点,
是椭圆上一点,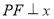 轴.若
轴.若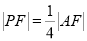 ,则该椭圆的离心率是( )
,则该椭圆的离心率是( ) (B)
(B) (C)
(C) (D)
(D)