题目内容
14.已知[x)表示大于x的最小整数,例如[3)=4,[-1,3)=-1,下列命题中正确的是( )①函数f(x)=[x)-x的值域是(0,1]
②若{an}是等差数列,则{[an)}也是等差数列
③若{an}是等比数列,则{[an)}也是等比数列
④若x∈(1,2017),则方程[x)-x=sin$\frac{π}{2}$x有1007个根.
| A. | ② | B. | ③④ | C. | ① | D. | ①④ |
分析 根据定义一一加以判断:对①考虑当x为整数和不为整数;对②可取特殊数列比如整数等差数列和非整数等差数列加以检验;对③也取特殊数列验证;对④因为x∈(1,2017),函数f(x)=[x)-x=sin$\frac{π}{2}$x的周期T=4,在(1,5]内有两个根,一个根x∈(4,5),另一个根x=5.即可得出.
解答 解:对①,当x为整数时,[x)=x+1,即[x)-x=1,当x不为整数时,0<[x)-x<1,所以函数f(x)=[x)-x的 值域是(0,1]即①对;
对②,当数列{an}是整数构成的等差数列,则数列{[an)}也是等差数列;当{an}不是整数构成的等差数列,则数列{[an)}不是等差数列.
例如:数列{an}:0.4,0.5,0.6,0.7,0.8,0.9,1.0,1.1;那么数列
{[an)}:1,1,1,1,1,1,2,2显然不是等差数列.故②错;
对③,可取等比数列{an}:1,2,4,8,16;则数列{[an)}为:2,3,5,9,17显然不是等比数列,故③错;
对④,因为x∈(1,2017),函数f(x)=[x)-x=sin$\frac{π}{2}$x的周期T=4,在(1,5]内有两个根,一个根x∈(4,5),另一个根x=5.因此方程[x)-x=sin$\frac{π}{2}$x在区间(1,2017)内共有504×2-1=1007个根.
故④对.
故选:D.
点评 本题考查了等差数列与等比数列的通项公式及其性质、函数的性质、函数与方程的关系,考查了推理能力与计算能力,属于难题.

练习册系列答案
相关题目
2.随机变量X~B(n,$\frac{1}{4}$),E(X)=3,则n=( )
| A. | 8 | B. | 12 | C. | 16 | D. | 20 |
6.一元二次不等式-x2+x+2>0的解集是( )
| A. | {x|x<-1或x>2} | B. | {x|x<-2或x>1} | C. | {x|-1<x<2} | D. | {x|-2<x<1} |
3.下列函数中,在其定义域内既是奇函数又是增函数的是( )
| A. | y=x3+x | B. | y=-$\frac{1}{x}$ | C. | y=sinx | D. | $y={({\frac{1}{2}})^x}-{2^x}$ |
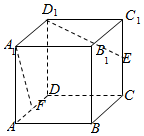 如图所示,在棱长为2的正方体ABCD-A1B1C1D1中,E,F分别是CC1,AD的中点,那么异面直线D1E和A1F所成角的余弦值等于$\frac{2}{5}$.
如图所示,在棱长为2的正方体ABCD-A1B1C1D1中,E,F分别是CC1,AD的中点,那么异面直线D1E和A1F所成角的余弦值等于$\frac{2}{5}$. 如图,已知动直线l过点$P(0,\frac{1}{2})$,且与圆O:x2+y2=1交于A、B两点.
如图,已知动直线l过点$P(0,\frac{1}{2})$,且与圆O:x2+y2=1交于A、B两点.