题目内容
已知 +
+ =1的焦点F1、F2,在直线l:x+y-6=0上找一点M,求以F1、F2为焦点,通过点M且长轴最短的椭圆方程.
=1的焦点F1、F2,在直线l:x+y-6=0上找一点M,求以F1、F2为焦点,通过点M且长轴最短的椭圆方程.
 +
+ =1的焦点F1、F2,在直线l:x+y-6=0上找一点M,求以F1、F2为焦点,通过点M且长轴最短的椭圆方程.
=1的焦点F1、F2,在直线l:x+y-6=0上找一点M,求以F1、F2为焦点,通过点M且长轴最短的椭圆方程.由 ,得F1(2,0),F2(-2,0),F1关于直线l的对称点F1/(6,4),连F1/F2交l于一点,即为所求的点M,∴2a=|MF1|+|MF2|=|F1/F2|=4
,得F1(2,0),F2(-2,0),F1关于直线l的对称点F1/(6,4),连F1/F2交l于一点,即为所求的点M,∴2a=|MF1|+|MF2|=|F1/F2|=4 ,∴a=2
,∴a=2 ,又c=2,∴b2=16,故所求椭圆方程为
,又c=2,∴b2=16,故所求椭圆方程为
 ,得F1(2,0),F2(-2,0),F1关于直线l的对称点F1/(6,4),连F1/F2交l于一点,即为所求的点M,∴2a=|MF1|+|MF2|=|F1/F2|=4
,得F1(2,0),F2(-2,0),F1关于直线l的对称点F1/(6,4),连F1/F2交l于一点,即为所求的点M,∴2a=|MF1|+|MF2|=|F1/F2|=4 ,∴a=2
,∴a=2 ,又c=2,∴b2=16,故所求椭圆方程为
,又c=2,∴b2=16,故所求椭圆方程为
略

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
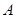 、
、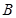 是椭圆
是椭圆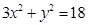 上的两点,点
上的两点,点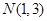 是线段
是线段 的中点,线段
的中点,线段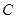 、
、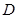 两点.
两点.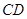 的中点
的中点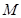 为圆心且与直线
为圆心且与直线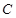 :
: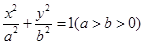 的离心率为
的离心率为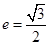 ,且过点
,且过点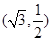 .
.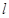 与椭圆
与椭圆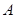 、
、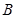 两点,若以
两点,若以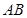 为直径的圆
为直径的圆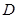 经过坐标原点.证明:圆
经过坐标原点.证明:圆 ,0)为右焦点的椭圆C,过点F垂直于
,0)为右焦点的椭圆C,过点F垂直于 轴的弦AB长为4.
轴的弦AB长为4. ,点P为椭圆C的右准线与
,点P为椭圆C的右准线与 的取值
的取值 范围.
范围.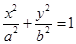
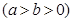 的一个焦点为F(1,0),且过点(2,0)
的一个焦点为F(1,0),且过点(2,0)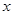 轴,又直线
轴,又直线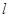 :
:
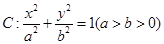 的长轴长为
的长轴长为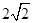 ,离
,离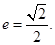
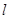 (斜率不等于零)与椭圆C交于点E,F,且
(斜率不等于零)与椭圆C交于点E,F,且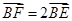 ,
,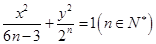 ,若椭圆的焦距为
,若椭圆的焦距为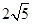 ,则
,则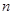 的取值集合为 。
的取值集合为 。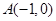 的直线
的直线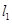 与过点
与过点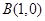 的直线
的直线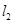 相交于点M,
相交于点M,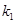 ,
,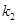 的乘积为定值
的乘积为定值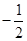 ,求点M的轨迹方程.
,求点M的轨迹方程.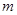 是两个正数
是两个正数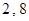 的等比中项,则圆锥曲线
的等比中项,则圆锥曲线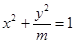 的离心率为 ( )
的离心率为 ( ) 或
或
