题目内容
设函数 ,
, .
.
(1)解方程: ;
;
(2)令 ,
, ,求证:
,求证:
(3)若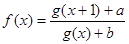 是实数集
是实数集 上的奇函数,且
上的奇函数,且 对任意实数
对任意实数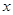 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.
(1) ;(2)参考解析;(3)
;(2)参考解析;(3)
解析试题分析:(1)由于函数 ,
, ,所以解方程
,所以解方程 .通过换元即可转化为解二次方程.即可求得结论.
.通过换元即可转化为解二次方程.即可求得结论.
(2)由于 即得到
即得到 .所以
.所以 .所以两个一组的和为1,还剩中间一个
.所以两个一组的和为1,还剩中间一个 .即可求得结论.
.即可求得结论.
(3)由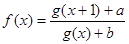 是实数集
是实数集 上的奇函数,可求得
上的奇函数,可求得 .又由于
.又由于 对任意实数
对任意实数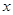 恒成立.该式的理解较困难,所以研究函数
恒成立.该式的理解较困难,所以研究函数 的单调性可得.函数
的单调性可得.函数 在实数集上是递增.集合奇函数,由函数值大小即可得到变量的大小,再利用基本不等式,从而得到结论.
在实数集上是递增.集合奇函数,由函数值大小即可得到变量的大小,再利用基本不等式,从而得到结论.
试题解析:(1) ,
, ,
,
(2) ,
, .
.
因为 ,
,
所以, ,
, .
. =
= .
.
(3)因为 是实数集上的奇函数,所以
是实数集上的奇函数,所以 .
. ,
, 在实数集上单调递增.
在实数集上单调递增.
由 得
得 ,又因为
,又因为 是实数集上的奇函数,所以,
是实数集上的奇函数,所以, ,
,
又因为 在实数集上单调递增,所以
在实数集上单调递增,所以
即 对任意的
对任意的 都成立,
都成立,
即 对任意的
对任意的 都成立,
都成立, .
.
考点:1.解方程的思想.2.函数的单调性.3.归纳推理的思想.4.基本不等式.

练习册系列答案
 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案
相关题目
 的定义域.
的定义域. (
( )
) 有3个不同的根,求实数
有3个不同的根,求实数 的取值范围;
的取值范围; 在
在 上恰有两个极值点
上恰有两个极值点 ,且满足
,且满足 ,若存在,求实数
,若存在,求实数 ,
, ,求函数的零点;
,求函数的零点; 上恰有一个零点,求
上恰有一个零点,求 的取值范围.
的取值范围.

 时,求
时,求 的极大值点;
的极大值点; 的图象
的图象 与函数
与函数 的图象
的图象 交于
交于 、
、 两点,过线段
两点,过线段 的中点做
的中点做 轴的垂线分别交
轴的垂线分别交 、
、 ,证明:
,证明: ,曲线
,曲线 在点
在点 处切线方程为
处切线方程为 .
. 的值;
的值; 的单调性,并求
的单调性,并求 ,
, ,
, .
. ,试判断并用定义证明函数
,试判断并用定义证明函数 的单调性;
的单调性; 时,求证函数
时,求证函数 (a>b>0)的左焦为F,右顶点为A,上顶点为B,O为坐标原点,M为椭圆上任意一点,过F,B,A三点的圆的圆心为(p,q).
(a>b>0)的左焦为F,右顶点为A,上顶点为B,O为坐标原点,M为椭圆上任意一点,过F,B,A三点的圆的圆心为(p,q). 的最小值为
的最小值为 ,求椭圆的方程.
,求椭圆的方程.