题目内容
已知 (
( )
)
(1)若方程 有3个不同的根,求实数
有3个不同的根,求实数 的取值范围;
的取值范围;
(2)在(1)的条件下,是否存在实数 ,使得
,使得 在
在 上恰有两个极值点
上恰有两个极值点 ,且满足
,且满足 ,若存在,求实数
,若存在,求实数 的值,若不存在,说明理由.
的值,若不存在,说明理由.
(1) ;(2)不存在,参考解析
;(2)不存在,参考解析
解析试题分析:(1)由已知 (
( ),若方程
),若方程 有3个不同的根,则可得到
有3个不同的根,则可得到 或
或 对两个方程分别讨论即可到结论.
对两个方程分别讨论即可到结论.
(2)在(1)的条件下,是否存在实数 ,使得
,使得 在
在 上恰有两个极值点
上恰有两个极值点 ,通过对函数求导,判断导函数的根的情况,通过换元使得等式简洁些.要满足
,通过对函数求导,判断导函数的根的情况,通过换元使得等式简洁些.要满足 ,由于
,由于 ,所以可得
,所以可得 ,通过验证根是否存在.即可得到结论.
,通过验证根是否存在.即可得到结论.
(1)解:由 得:
得: 或
或
可得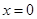 或
或 且
且
∵方程 有3个不同的根,
有3个不同的根,
∴方程 有两个不同的根
有两个不同的根
∴
又∵ ,且要保证
,且要保证 能取到0∴
能取到0∴ 即
即
∴ .
.
(2)解:∵
令 ,设
,设
∴
 ∵
∵ ∴
∴ ∴
∴


∵ ∴
∴ ,
, ∴
∴
∴存在 ,使得
,使得 ,另外有
,另外有 ,使得
,使得
假设存在实数 ,使得
,使得 在
在 上恰有两个极值点
上恰有两个极值点 ,且满足
,且满足
则存在 ,使得
,使得 ,另外有
,另外有 ,即
,即
∴ ,∴
,∴ ,即
,即
即 (*)
(*)
设
∴
∵ ∴
∴
∴ ∴
∴ 在
在 上是增函数
上是增函数
∴

练习册系列答案
相关题目
 的图象为C1,C1关于点A(2,1)对称的图象为C2,C2对应的函数为g(x).
的图象为C1,C1关于点A(2,1)对称的图象为C2,C2对应的函数为g(x). k元.假设座位等距分布,且至少有两个座位,所有座位都视为点,且不考虑其他因素,记转盘的总造价为y元.
k元.假设座位等距分布,且至少有两个座位,所有座位都视为点,且不考虑其他因素,记转盘的总造价为y元. (
( ).
). 的定义域和值域均是
的定义域和值域均是 ,求实数
,求实数 的值;
的值; 上是减函数,且对任意的
上是减函数,且对任意的 ,
,
 ,总有
,总有 ,求实数
,求实数 中,
中, ,点
,点 是边
是边 上的动点,动点
上的动点,动点 满足
满足 (点
(点 按逆时针方向排列).
按逆时针方向排列).
 ,求
,求 的长;
的长; ,求△
,求△ 面积的最大值.
面积的最大值. 是偶函数.
是偶函数. 的值;
的值; ,若函数
,若函数 与
与 的图象有且只有一个公共点,求实数a的取值范围.
的图象有且只有一个公共点,求实数a的取值范围. ,
, .
. ;
; ,
, ,求证:
,求证:
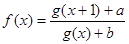 是实数集
是实数集 上的奇函数,且
上的奇函数,且 对任意实数
对任意实数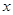 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.
 的奇偶性;
的奇偶性; 和
和 上的增减性;
上的增减性; 满足:
满足: ,试证明:
,试证明: .
.