题目内容
已知函数 ,曲线
,曲线 在点
在点 处切线方程为
处切线方程为 .
.
(1)求 的值;
的值;
(2)讨论 的单调性,并求
的单调性,并求 的极小值。
的极小值。
(1)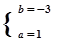 ;(2)
;(2)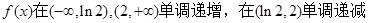 .
.
当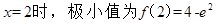 .
.
解析试题分析:(1)对函数数求导,利用切线的斜率为2,切点为曲线与切线的交点,可得 的值.(2)利用导函数的,构建不等式讨论
的值.(2)利用导函数的,构建不等式讨论 的单调性,并利用单调区间判断极值.
的单调性,并利用单调区间判断极值.
试题解析:
解: 2分
2分
因为在点 处切线方程为
处切线方程为 .
.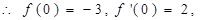
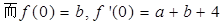
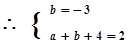 4分解得:
4分解得: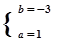 5分
5分
(2)由(I)知,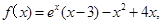
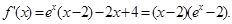 7分
7分
令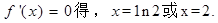 9分
9分
从而当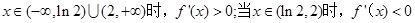 。 11分
。 11分
故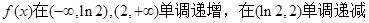 . 12分
. 12分
当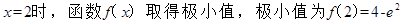 14分
14分
考点:利用导数示函数的单调区间和极值.

练习册系列答案
相关题目

 的最小值;
的最小值;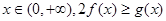 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围. 中,
中, ,点
,点 是边
是边 上的动点,动点
上的动点,动点 满足
满足 (点
(点 按逆时针方向排列).
按逆时针方向排列).
 ,求
,求 的长;
的长; ,求△
,求△ 面积的最大值.
面积的最大值. .
.

 的解集;
的解集;
 ,若
,若 对任意的
对任意的 都成立,求
都成立,求 的取值范围.
的取值范围. ,
, .
. ;
; ,
, ,求证:
,求证:
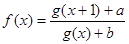 是实数集
是实数集 上的奇函数,且
上的奇函数,且 对任意实数
对任意实数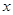 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.
 .
. 时,判断
时,判断 在
在 的单调性,并用定义证明;
的单调性,并用定义证明; ,不等式
,不等式 恒成立,求
恒成立,求 的取值范围;
的取值范围; .
. 的单调区间;
的单调区间; ,存在唯一的
,存在唯一的 ,使
,使 ;
; 的函数为
的函数为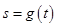 ,证明:当
,证明:当 时,有
时,有 .
. 是定义域为
是定义域为 的偶函数.当
的偶函数.当 时,
时, 若关于
若关于 的方程
的方程
 有且只有7个不同实数根,则
有且只有7个不同实数根,则 的值是.
的值是. ;
; ;
; ;
; .
.