题目内容
已知函数 ,
, ,
, .
.
(1)若 ,试判断并用定义证明函数
,试判断并用定义证明函数 的单调性;
的单调性;
(2)当 时,求证函数
时,求证函数 存在反函数.
存在反函数.
(1)增函数;(2)参考解析
解析试题分析:(1)当 时,
时,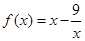 ,
, .通过函数的单调性的定义可证得函数
.通过函数的单调性的定义可证得函数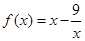 ,
, 单调递增.
单调递增.
(2)由 ,所以将x的区间分为两类即
,所以将x的区间分为两类即 和
和 .所以函数
.所以函数 .由(1)可得函数
.由(1)可得函数 是递增函数.应用单调性的定义同样可得函数
是递增函数.应用单调性的定义同样可得函数 是递增.根据反函数的定义可得函数存在反函数.
是递增.根据反函数的定义可得函数存在反函数.
试题解析:(1)判断:若 ,函数
,函数 在
在 上是增函数.
上是增函数.
证明:当 时,
时,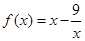 ,
, 在
在 上是增函数.2分
上是增函数.2分
在区间 上任取
上任取 ,设
,设 ,
,
所以 ,即
,即 在
在 上是增函数.6分
上是增函数.6分
(2)因为 ,所以
,所以 8分
8分
当 时,
时, 在
在 上是增函数,9分
上是增函数,9分
证明:当 时,
时, 在
在 上是增函数(过程略)11分
上是增函数(过程略)11分 在在
在在 上也是增函数,当
上也是增函数,当 时,
时,
 上是增函数12分
上是增函数12分
所以任意一个 ,均能找到唯一的
,均能找到唯一的 和它对应,
和它对应,
所以

 时,
时, 存在反函数14分
存在反函数14分
考点:1.函数的单调性.2.函数单调性的定义.3.反函数的概念.

练习册系列答案
相关题目
 是偶函数.
是偶函数. 的值;
的值; ,若函数
,若函数 与
与 的图象有且只有一个公共点,求实数a的取值范围.
的图象有且只有一个公共点,求实数a的取值范围. ,
, .
. ;
; ,
, ,求证:
,求证:
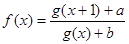 是实数集
是实数集 上的奇函数,且
上的奇函数,且 对任意实数
对任意实数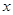 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围. ,
, .
. ,求证:函数
,求证:函数 是
是 上的奇函数;
上的奇函数; 上没有零点,求实数
上没有零点,求实数 的取值范围.
的取值范围. .
. 的单调区间;
的单调区间; ,存在唯一的
,存在唯一的 ,使
,使 ;
; 的函数为
的函数为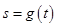 ,证明:当
,证明:当 时,有
时,有 .
. 表示的曲线是双曲线;命题
表示的曲线是双曲线;命题 函数
函数 在区间
在区间 上为增函数,若“
上为增函数,若“

 ”为真命题,“
”为真命题,“
 的取值范围.
的取值范围.
 的奇偶性;
的奇偶性; 和
和 上的增减性;
上的增减性; 满足:
满足: ,试证明:
,试证明: .
. .
.