题目内容

16．直线y=x+3与抛物线x2=4y所围成的封闭图形的面积等于$\frac{64}{3}$．

分析 本题考查的知识点是定积分的几何意义，首先我们要联立两个曲线的方程，判断他们的交点，以确定积分公式中x的取值范围，再根据定积分的几何意义，得到所求图形的面积．

解答 解：由直线y=x+3与抛物线x2=4y，联立解得，x1=-2，x2=6．
故所求图形的面积为S=∫-26（x+3-$\frac{1}{4}$x2）dx
=（$\frac{1}{2}{x}^{2}$+3x-$\frac{1}{12}{x}^{3}$）|-26=$\frac{64}{3}$，
故答案为：$\frac{64}{3}$．

点评 本题考查定积分的运用，解题的关键是确定积分区间与被积函数．

练习册系列答案
相关题目
6．已知双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1（a＞0，b＞0）$与抛物线y2=8x有一个公共的焦点F．设这两曲线的一个交点为P，若|PF|=5，则点P的横坐标是3；该双曲线的渐近线方程为y=±$\sqrt{3}$x．
7．已知点P（$\sqrt{3}$，$\frac{1}{2}$）在椭圆E：$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）上，F为右焦点，PF垂直于x轴，A，B，C，D为椭圆上四个动点，且AC，BD交于原点O．
（Ⅰ）求椭圆E的方程；
（Ⅱ）设A（x1，y1），B（x2，y2），满足$\frac{{{y}_{1}y}_{2}}{\overrightarrow{OA}•\overrightarrow{OB}}$=$\frac{1}{5}$，判断kAB+kBC的值是否为定值，若是，求出此定值，并求出四边形ABCD面积的最大值，否则请说明理由．
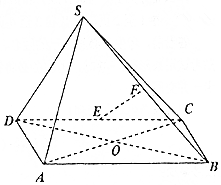4．如图，在四棱锥S-ABCD中，四边形ABCD是菱形，∠BAD=60°，AC交BC于点O，△SBD是边长为2的正三角形，SA=$\sqrt{3}$，E，F分别是CD，SB的中点．
（Ⅰ）求证：EF∥平面SAD；
（Ⅱ）求证：BD⊥平面SAC；
（Ⅲ）求直线AB与平面SBD所成角的正弦值．
11．△ABC的内角A，B，C的对边分别是a，b，c，若a2=（b+c）2-4，△ABC的面积为$\sqrt{3}$，则A等于（　　）
A．30°B．60°C．150°D．120°
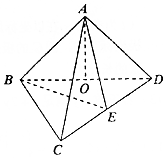1．如图，在三棱锥A-BCD中，顶点A在底面BCD上的射影O在棱BD上，AB=AD=$\sqrt{2}$，BC=BD=2，∠CBD=90°，E为CD的中点．
（Ⅰ）求证：AD⊥平面ABC；
（Ⅱ）求直线AC与平面ABE所成角的正弦值；
（Ⅲ）求二面角B-AE-C的余弦值．
8．某校高三年级某班的数学课外活动小组有6名男生，4名女生，从中选出4人参加数学竞赛考试，用X表示其中男生的人数．
（Ⅰ）请列出X的分布列并求数学期望；
（Ⅱ）根据所列的分布列求选出的4人中至少有3名男生的概率．
13．设函数f（x）=$\sqrt{|x-1|+|x-2|-a}$．
（1）当a=5时，求函数f（x）的定义域；
（2）若函数f（x）的定义域为R，试求a的取值范围．
14．等差数列{an}的各项均为正数，a1=3，前n项和为Sn，{bn}为等比数列，b1=1，且b2S2=64，b3S3=960．
（1）求an与bn；
（2）证明：$\frac{1}{S1}$+$\frac{1}{S2}$+…+$\frac{1}{Sn}$＜$\frac{3}{4}$．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网