题目内容
正方体 --
-- ,E、F分别是
,E、F分别是 、
、 的中点,p是
的中点,p是 上的动点(包括端点),过E、D、P作正方体的截面,若截面为四边形,则P的轨迹是
上的动点(包括端点),过E、D、P作正方体的截面,若截面为四边形,则P的轨迹是
A、线段 B、线段
B、线段
C、线段 和一点
和一点 D、线段
D、线段 和一点C
和一点C
 --
-- ,E、F分别是
,E、F分别是 、
、 的中点,p是
的中点,p是 上的动点(包括端点),过E、D、P作正方体的截面,若截面为四边形,则P的轨迹是
上的动点(包括端点),过E、D、P作正方体的截面,若截面为四边形,则P的轨迹是A、线段
 B、线段
B、线段
C、线段
 和一点
和一点 D、线段
D、线段 和一点C
和一点CC
【错解分析】学生的空间想象能力不足,不能依据平面的基本定理和线面平行定理作两平面的交线。
【正解】如图当点P在线段
 上移动时,易由线面平行的性质定理知:直线DE平行于平面
上移动时,易由线面平行的性质定理知:直线DE平行于平面 ,则过DE的截面DEP与平面
,则过DE的截面DEP与平面 的交线必平行,因此两平面的交线为过点P与DE平行的直线,由于点P在线段CF上故此时过P与DE平行的直线与直线
的交线必平行,因此两平面的交线为过点P与DE平行的直线,由于点P在线段CF上故此时过P与DE平行的直线与直线 的交点在线段
的交点在线段 上,故此时截面为四边形(实质上是平行四边形),特别的当P点恰为点F时,此时截面为
上,故此时截面为四边形(实质上是平行四边形),特别的当P点恰为点F时,此时截面为 也为平行四边形,当点P在线段
也为平行四边形,当点P在线段 上时如图分别延长DE、DP交
上时如图分别延长DE、DP交 、
、 于点H、G则据平面基本定理知点H、G既在平截面DEP内也在平面
于点H、G则据平面基本定理知点H、G既在平截面DEP内也在平面 内,故GH为两平面的交线,连结GH分别交
内,故GH为两平面的交线,连结GH分别交 、
、 于点K、N(注也有可能交在两直线的延长线上),再分别连结EK、KN、PN即得截面为DEKNP此时为五边形。故选C
于点K、N(注也有可能交在两直线的延长线上),再分别连结EK、KN、PN即得截面为DEKNP此时为五边形。故选C


练习册系列答案
 夺冠金卷全能练考系列答案
夺冠金卷全能练考系列答案
相关题目
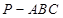 中,
中,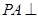 底面
底面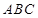 ,
,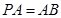 ,
,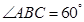 ,
,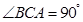 ,点
,点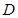 ,
,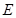 分别在棱
分别在棱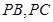 上,且
上,且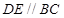
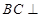 平面
平面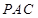 ;
;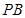 的中点时,求
的中点时,求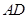 与平面
与平面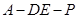 为直二面角?并说明理由.
为直二面角?并说明理由.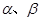 和两条不重合的直线
和两条不重合的直线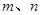 ,有下列四个命题:
,有下列四个命题: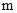 //
//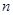 ,
,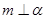 ,则
,则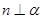 ; ②若
; ②若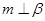 ,则
,则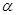 //
//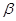 ;
;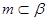 ,则
,则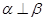 ; ④若
; ④若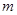 //
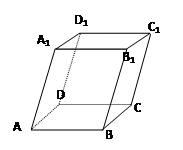
//
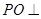 平面
平面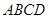 ,点
,点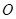 在
在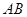 上,
上,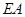 ∥
∥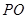 ,四边形
,四边形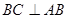 ,
,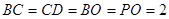 ,
,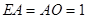
 平面
平面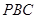 ;
;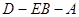 的余弦值;
的余弦值;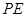 上是否存在点
上是否存在点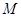 ,使
,使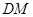 ∥平面
∥平面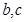 表示两条直线,
表示两条直线,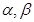 表示两个平面,则下列命题是真命题的是( )
表示两个平面,则下列命题是真命题的是( ) ,
, ∥
∥ ,则
,则

 ,则
,则

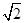 ,F是BC的中点.
,F是BC的中点.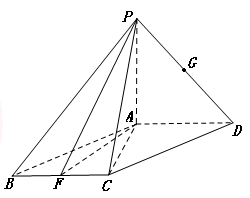
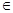 平面CC1D1D,且PC=PD=
平面CC1D1D,且PC=PD=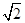 .
.
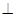 平面PBC;
平面PBC;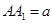 ,当a为何值时,PC//平面
,当a为何值时,PC//平面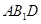 .
. 是三个不同的平面,给出下列四个命题:
是三个不同的平面,给出下列四个命题: ,
, ,则
,则 ②若
②若 ,
, ,
,
 ,
, ,则
,则 ④若
④若 ,
,  ,则
,则