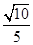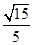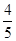题目内容
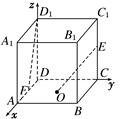
(本小题12分) 如图四棱柱ABCD-A1B1C1D1的底面ABCD为正方形,侧棱与底边长均为a,
且∠A1AD=∠A1AB=60°。
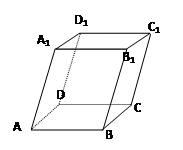
①求证四棱锥 A1-ABCD为正四棱锥;
②求侧棱AA1到截面B1BDD1的距离;
③求侧面A1ABB1与截面B1BDD1的锐二面角大小。
且∠A1AD=∠A1AB=60°。

①求证四棱锥 A1-ABCD为正四棱锥;
②求侧棱AA1到截面B1BDD1的距离;
③求侧面A1ABB1与截面B1BDD1的锐二面角大小。
(1)因为Rt△ABD的外心是斜边BD的中点,所以O是底面正方形ABCD的中心,因此证明。
(2) a
a
(3)arctan 。
。
(2)
 a
a(3)arctan
 。
。试题分析:(1)由AA1=AD=AB,及∠A1AD=∠A1AB=60°
 △A1AD、△AA1B都是正三角形,从而AA1=A1D=A1B,设A1在底面ABCD的射影为O,则由斜线长相等推出射影长也相等,所以O是Rt△ABD的外心,因为Rt△ABD的外心是斜边BD的中点,所以O是底面正方形ABCD的中心。所以四棱锥A1—ABCD是正四棱锥。
△A1AD、△AA1B都是正三角形,从而AA1=A1D=A1B,设A1在底面ABCD的射影为O,则由斜线长相等推出射影长也相等,所以O是Rt△ABD的外心,因为Rt△ABD的外心是斜边BD的中点,所以O是底面正方形ABCD的中心。所以四棱锥A1—ABCD是正四棱锥。
(2)由DB⊥平面AA1O
 截面BB1D1D⊥平面AA1O
截面BB1D1D⊥平面AA1O 点O与侧棱AA1的距离d等于AA1和截面BB1D1D之间的距离。取AA1的中点M,则OM∥A1C,且OM⊥AA1,OM=
点O与侧棱AA1的距离d等于AA1和截面BB1D1D之间的距离。取AA1的中点M,则OM∥A1C,且OM⊥AA1,OM= A1C=
A1C= a,∴所求距离为
a,∴所求距离为 a。
a。(3)注意到所求二面角的棱是B1B,由M是AA1的中点
 MB⊥AA1,B1B∥AA1
MB⊥AA1,B1B∥AA1 MB⊥B1B,又DB⊥AA1,AA1//B1B
MB⊥B1B,又DB⊥AA1,AA1//B1B DB⊥B1B,
DB⊥B1B,
∴∠MBD是所求二面角的平面角。不妨设AB=a=2,则BD=2
 ,MB=MD=
,MB=MD= ,
,∴tanMBD=
 。
。∴侧面A1ABB1与截面B1BDD1的夹角为arctan
 。
。点评:对于立体几何中的角和距离的求解是高考的一个方向,那么解决这类问题一般可以从两个角度来做,一个就是利用几何性质,结合定理和推论来了得到,另一个就是建立直角坐标系,通过法向量和直线的方向向量来表示得到,属于中档题。

练习册系列答案
相关题目
 中
中 平面
平面 ,
, ,底面为直角梯形,
,底面为直角梯形,
 分别是
分别是 的中点.
的中点.
 // 平面
// 平面 ;
; 与底面
与底面 到平面
到平面 中,
中,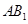 与
与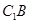 所成的角为( )
所成的角为( )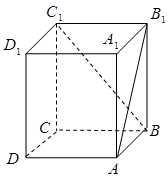

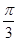
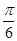
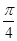
 中,底面ABCD是一直角梯形,
中,底面ABCD是一直角梯形, ,
, ,
, ,且PA=AD=DC=
,且PA=AD=DC= AB=1.
AB=1.
 平面
平面
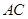 与
与 所成角的余弦值
所成角的余弦值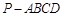 中,
中,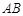 ∥
∥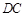 ,
,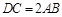 ,
,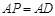 ,
,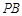 ⊥
⊥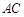 ,
,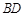 ⊥
⊥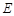 为
为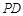 的中点.
的中点.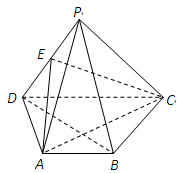
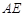 ∥平面
∥平面 ;
;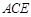 .
. 与矩形
与矩形 所在的平面互相垂直,将
所在的平面互相垂直,将 沿
沿 翻折,翻折后的点E恰与BC上的点P重合.设
翻折,翻折后的点E恰与BC上的点P重合.设 ,
, ,
, ,则当
,则当 __时,
__时, 有最小值.
有最小值.
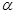 ,
,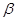 ,
,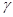 是三个互不重合的平面,
是三个互不重合的平面,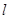 是一条直线,下列命题中正确命题是( )
是一条直线,下列命题中正确命题是( ) ,
,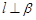 ,则
,则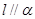
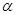 的距离相等,则
的距离相等,则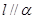
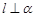 ,
,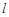 ∥
∥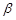 ,则
,则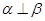
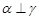 ,则
,则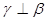
 --
-- ,E、F分别是
,E、F分别是 、
、 的中点,p是
的中点,p是 B、线段
B、线段
 D、线段
D、线段