题目内容

现有2名女教师和1名男教师参加说题比赛，共有2道备选题目，若每位选手从中有放回地随机选出一道题进行说题，其中恰有一男一女抽到同一道题的概率为（　　）
A、
1
3
B、
2
3
C、
1
2
D、
3
4
考点：古典概型及其概率计算公式
专题：计算题,概率与统计
分析：列举基本事件，利用古典概型概率公式求解即可．
解答： 解：设两道题分别为A，B题，所以抽取情况共有：AAA，AAB，ABA，ABB，BAA，BAB，BBA，BBB，其中第1个，第2个分别是两个女教师抽取的题目，
第3个表示男教师抽取的题目，一共有8种；其中满足恰有一男一女抽到同一题目的事件有：ABA，ABB，BAA，BAB，共4种；
故所求事件的概率为
1
2
．
故选：C．
点评：列举法是确定基本事件的常用方法．如果一个事件有n种可能，而且这些事件的可能性相同，其中事件A出现m种结果，那么事件A的概率P（A）=
m
n
．
练习册系列答案
相关题目
已知方程|x2-a|-x+2=0（a＞0）有两个不等的实数根，则实数a的取值范围是（　　）
A、0＜a＜4B、a＞4
C、0＜a＜2D、a＞2
P为椭圆
x2
4
+
y2
3
=1上一点，F1、F2为该椭圆的两个焦点，若∠F1PF2=60°，则
.
PF1
•
.
PF2
等于（　　）
A、3
B、
3
C、2
3
D、2
已知函数f（x）对?x∈R满足f（x）=-f（2-x），且在[1，+∞）上递增，若g（x）=f（1+x），且2g（log2a）-3g（1）≤g（log 
1
2
a），则实数a的范围为（　　）
A、（0，2]
B、（0，
1
2
]
C、[
1
2
，2]
D、[1，2]
已知定义在R上的函数f（x），对任意x∈R，都有f（x+4）=f（x）+f（2）成立，若函数y=f（x+1）的图象关于直线x=-1对称，则f（2014）的值为（　　）
A、2014B、-2014
C、0D、4
若x+y=0，则2x+2y的最小值是（　　）
A、
1
2
B、1
C、2
D、4
已知xi＞0（i=1，2，3，…n），我们知道有（x1+x2）（
1
x1
+
1
x2
）≥4成立．
（Ⅰ）请猜测（x1+x2+x3）（
1
x1
+
1
x2
+
1
x3
）≥？；（x1+x2+x3+x4）（
1
x1
+
1
x2
+
1
x3
+
1
x4
）≥？
（Ⅱ）由上述几个不等式，请你猜测与x1+x2+…+xn和
1
x1
+
1
x2
+…+
1
xn
（N≥2，n∈N*）；（有关的不等式，并用数学归纳法证明．
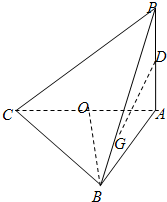如图，在三棱锥P-ABC中，PA⊥平面ABC，AB⊥AC．
（Ⅰ）求证：AC⊥PB；
（Ⅱ）设O，D分别为AC，AP的中点，点G为△OAB内一点，且满足
OG
=
1
3
(
OA
+
OB
)，求证：DG∥面PBC；
（Ⅲ）若AB=AC=2，PA=4，求二面角A-PB-C的余弦值．
已知数列{an}满足：a1=
8
9
，an+1=an+
8(n+1)
(2n+1)2(2n+3)2

（1）求a2、a3；
（2）猜想{an}的通项公式，并用数学归纳法证明．
（3）求证：a1+a2+…+an＞n-
1
4
（n∈N*）

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网