题目内容
14.在平面直角坐标系xOy中,直线l的参数方程为$\left\{\begin{array}{l}{x=1+\frac{t}{2}}\\{y=2+\frac{\sqrt{3}}{2}t}\end{array}\right.$ (t为参数).以原点为极点,x轴正半轴为极轴建立极坐标系,曲线C的极坐标方程是ρ=2$\sqrt{3}$sinθ.(I)求出直线l的普通方程与曲线C的直角坐标方程;
(II)设直线l与曲线C的交点为A,B,求|AB|的值.
分析 (1)使用加减消元法消去参数t即得直线l的普通方程,将极坐标方程两边同乘ρ即可得到曲线C的直角坐标方程;
(2)求出曲线C的圆心到直线l的距离,利用垂径定理求出|AB|.
解答 解:(I)∵$\left\{\begin{array}{l}{x=1+\frac{t}{2}}\\{y=2+\frac{\sqrt{3}}{2}t}\end{array}\right.$ (t为参数),∴$\sqrt{3}$x-y=$\sqrt{3}-2$,
即直线l的普通方程为$\sqrt{3}x$-y+2-$\sqrt{3}$=0.
由ρ=2$\sqrt{3}$sinθ得ρ2=2$\sqrt{3}$ρsinθ,即x2+y2=2$\sqrt{3}$y.
∴曲线C的直角坐标方程为x2+y2=2$\sqrt{3}$y.即x2+(y-$\sqrt{3}$)2=3.
(II)由(1)知曲线C的圆心为(0,$\sqrt{3}$),半径r=$\sqrt{3}$.
∴曲线C的圆心到直线l的距离d=$\frac{2\sqrt{3}-2}{2}$=$\sqrt{3}-1$.
∴|AB|=2$\sqrt{{r}^{2}-{d}^{2}}$=2$\sqrt{3-(\sqrt{3}-1)^{2}}$=2$\sqrt{2\sqrt{3}-1}$.
点评 本题考查了参数方程,极坐标方程与普通方程的转化,直线与圆的位置关系,属于基础题.

练习册系列答案
相关题目
4.“m>0”是“方程$\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{m}$=1表示椭圆”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
9.乘积(x+y+z)(a-b+c)(m-n+p+q-3)展开后共有( )项.
| A. | 11 | B. | 12 | C. | 45 | D. | 120 |
3.设sin(x+y)=a,sin(x-y)=b,则sinxcosy等于( )
| A. | a+b | B. | a-b | C. | $\frac{a+b}{2}$ | D. | $\frac{a-b}{2}$ |
6.“x>0”是“x≥0”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
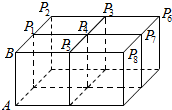 如图,四个完全相同的长方体排成一个直四棱柱:每个长方体底面为边长1的正方形,侧棱AB长为2,Pi(i=1,2…)是上底面上其余的八个点,则$\overrightarrow{AB}$•$\overrightarrow{A{P}_{i}}$(i=1,2,…)的不同值的个数为( )
如图,四个完全相同的长方体排成一个直四棱柱:每个长方体底面为边长1的正方形,侧棱AB长为2,Pi(i=1,2…)是上底面上其余的八个点,则$\overrightarrow{AB}$•$\overrightarrow{A{P}_{i}}$(i=1,2,…)的不同值的个数为( )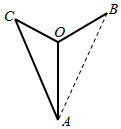 如图是某设计师设计的Y型饰品的平面图,其中支架OA,OB,OC两两成120°,OC=1,AB=OB+OC,且OA>OB,现设计师在支架OB上装点普通珠宝,普通珠宝的价值为M,且M与OB长成正比,比例系数为k(k为正常数):在△AOC区域(阴影区域)内镶嵌名贵珠宝,名贵珠宝的价值为N,且N与△AOC的面积成正比,比例系数为4$\sqrt{3}$k,设OA=x,OB=y.
如图是某设计师设计的Y型饰品的平面图,其中支架OA,OB,OC两两成120°,OC=1,AB=OB+OC,且OA>OB,现设计师在支架OB上装点普通珠宝,普通珠宝的价值为M,且M与OB长成正比,比例系数为k(k为正常数):在△AOC区域(阴影区域)内镶嵌名贵珠宝,名贵珠宝的价值为N,且N与△AOC的面积成正比,比例系数为4$\sqrt{3}$k,设OA=x,OB=y.