题目内容
已知f(x)=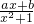 为定义在R上的奇函数,且f(1)=
为定义在R上的奇函数,且f(1)=
(1)求f(x)的解析式;
(2)判断并证明y=f(x)在(-1,0)上的单调性.
解:(1)因为f(x)=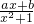 为定义在R上的奇函数,且f(1)=
为定义在R上的奇函数,且f(1)= ,
,
所以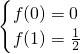 ,即
,即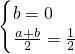 ,解得:
,解得: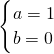 .
.
所以,f(x)= .
.
(2)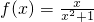 在(-1,0)上为单调增函数.
在(-1,0)上为单调增函数.
证明:任取x1,x2∈(-1,0)且x1<x2
则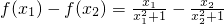
=
=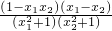 .
.
因为x1,x2∈(-1,0)且x1<x2,
所以1-x1x2>0,x1-x2<0.
所以,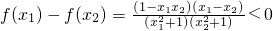 .
.
即f(x1)<f(x2).
所以,函数y=f(x)在(-1,0)上的单调递增.
分析:(1)函数是定义在实数集上的奇函数,由f(0)=0,f(1)= 联立方程组可求a和b的值,则函数解析式可求;
联立方程组可求a和b的值,则函数解析式可求;
(2)直接运用函数单调性的定义证明函数y=f(x)在(-1,0)上的单调性.
点评:本题考查了用赋值法求函数的解析式,考查了函数的单调性,利用函数的单调性定义证明函数的单调性时,步骤是首先在给定的区间内任取两个自变量的值x1,x2,并且规定大小,然后把它们对应的函数值作差,目的是判断差式的符号,从而得到f(x1)和f(x2)的大小,最后根据定义得结论,此题是中档题.
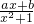 为定义在R上的奇函数,且f(1)=
为定义在R上的奇函数,且f(1)= ,
,所以
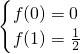 ,即
,即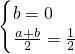 ,解得:
,解得: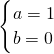 .
.所以,f(x)=
 .
.(2)
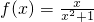 在(-1,0)上为单调增函数.
在(-1,0)上为单调增函数.证明:任取x1,x2∈(-1,0)且x1<x2
则
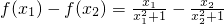
=

=
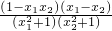 .
.因为x1,x2∈(-1,0)且x1<x2,
所以1-x1x2>0,x1-x2<0.
所以,
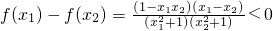 .
.即f(x1)<f(x2).
所以,函数y=f(x)在(-1,0)上的单调递增.
分析:(1)函数是定义在实数集上的奇函数,由f(0)=0,f(1)=
 联立方程组可求a和b的值,则函数解析式可求;
联立方程组可求a和b的值,则函数解析式可求;(2)直接运用函数单调性的定义证明函数y=f(x)在(-1,0)上的单调性.
点评:本题考查了用赋值法求函数的解析式,考查了函数的单调性,利用函数的单调性定义证明函数的单调性时,步骤是首先在给定的区间内任取两个自变量的值x1,x2,并且规定大小,然后把它们对应的函数值作差,目的是判断差式的符号,从而得到f(x1)和f(x2)的大小,最后根据定义得结论,此题是中档题.

练习册系列答案
相关题目
已知f(x)是定义在R上的不恒为零的函数,且对于任意实数a,b∈R满足:f(a•b)=af(b)+bf(a),f(2)=2,an=
(n∈N*),bn=
(n∈N*)
考察下列结论:①f(0)=f(1);②数列{an}为等比例数列;③数列{bn}为等差数列.
其中正确的结论是( )
| f(2n) |
| n |
| f(2n) |
| 2n |
考察下列结论:①f(0)=f(1);②数列{an}为等比例数列;③数列{bn}为等差数列.
其中正确的结论是( )
| A、①②③ | B、①③ | C、①② | D、②③ |
已知f(x)是定义在R上的偶函数,f(x)在x∈[0,+∞)上为增函数,且f(
)=0,则不等式f(log
x)>0的解集为( )
| 1 |
| 3 |
| 1 |
| 8 |
A、(0,
| ||
| B、(2,+∞) | ||
C、(
| ||
D、[0,
|