题目内容
圆:x2+y2-4x+6y=0和圆:x2+y2-6y=0交于A,B两点,则AB的垂直平分线的方程是
- A.x+y+3=0
- B.2x-y-5=0
- C.3x+y-3=0
- D.4x-3y+7=0
C
分析:通过平面几何的知识可知AB的垂直平分线即是两圆的连心线,进而通过两圆的方程分别求得圆心坐标,利用两点式求得直线的方程.
解答:整理两圆的方程可得(x-2)2+(y+3)2=13,x2+(y-3)2=9
∴两圆的圆心分别为(2,-3),(0,3)
由平面几何知识知AB的垂直平分线就是连心线
∴连心线的斜率为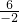 =-3
=-3
∴直线方程为y-3=-3x,整理得3x+y-3=0
故选C
点评:本题主要考查了圆与圆的位置关系及其判定.考查了考生分析问题和解决问题的能力.
分析:通过平面几何的知识可知AB的垂直平分线即是两圆的连心线,进而通过两圆的方程分别求得圆心坐标,利用两点式求得直线的方程.
解答:整理两圆的方程可得(x-2)2+(y+3)2=13,x2+(y-3)2=9
∴两圆的圆心分别为(2,-3),(0,3)
由平面几何知识知AB的垂直平分线就是连心线
∴连心线的斜率为
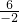 =-3
=-3∴直线方程为y-3=-3x,整理得3x+y-3=0
故选C
点评:本题主要考查了圆与圆的位置关系及其判定.考查了考生分析问题和解决问题的能力.

练习册系列答案
 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案
相关题目