题目内容
已知椭圆C: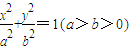 的左焦点为F(-1,0),离心率为
的左焦点为F(-1,0),离心率为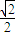 ,过点F的直线l与椭圆C交于A、B两点.
,过点F的直线l与椭圆C交于A、B两点.(Ⅰ)求椭圆C的方程;
(Ⅱ)设过点F不与坐标轴垂直的直线交椭圆C于A、B两点,线段AB的垂直平分线与x轴交于点G,求点G横坐标的取值范围.
【答案】分析:(Ⅰ)由题意可知:c=1,a2=b2-c2,e= ,由此能够求出椭圆的方程.
,由此能够求出椭圆的方程.
(II)设直线AB的方程为y=k(x+1)(k≠0),由 ,得(1+2k2)x2+4k2x+2k2-2=0.由直线AB过椭圆的左焦点F,记A(x1,y1),B(x2,y2),AB的中点N(x,y),x1+x2=
,得(1+2k2)x2+4k2x+2k2-2=0.由直线AB过椭圆的左焦点F,记A(x1,y1),B(x2,y2),AB的中点N(x,y),x1+x2= ,x=
,x= ,垂直平分线NG的方程为y-y=-
,垂直平分线NG的方程为y-y=- ,由此能求出点G横坐标的取值范围.
,由此能求出点G横坐标的取值范围.
解答:解:(Ⅰ)由题意可知:c=1,a2=b2-c2,e= …(2分)
…(2分)
解得:a= ,b=1(3分)
,b=1(3分)
故椭圆的方程为: =1(4分)
=1(4分)
(II)设直线AB的方程为y=k(x+1)(k≠0),(5分)
联立,得 ,
,
整理得(1+2k2)x2+4k2x+2k2-2=0(7分)
∵直线AB过椭圆的左焦点F∴方程有两个不等实根.(8分)
记A(x1,y1),B(x2,y2),AB的中点N(x,y)
则x1+x2= (9分)
(9分)
x= (10分)
(10分)
垂直平分线NG的方程为y-y=- ,(11分)
,(11分)
令y=0,得xG=x+ky=-
=- .(12分)
.(12分)
∵k≠0,∴- <0(13分)
<0(13分)
∴点G横坐标的取值范围为(- ,0).(14分)
,0).(14分)
点评:本题主要考查直线与圆锥曲线的综合应用能力,综合性强,是高考的重点,易错点是知识体系不牢固.本题具体涉及到轨迹方程的求法及直线与椭圆的相关知识,解题时要注意合理地进行等价转化.
 ,由此能够求出椭圆的方程.
,由此能够求出椭圆的方程.(II)设直线AB的方程为y=k(x+1)(k≠0),由
 ,得(1+2k2)x2+4k2x+2k2-2=0.由直线AB过椭圆的左焦点F,记A(x1,y1),B(x2,y2),AB的中点N(x,y),x1+x2=
,得(1+2k2)x2+4k2x+2k2-2=0.由直线AB过椭圆的左焦点F,记A(x1,y1),B(x2,y2),AB的中点N(x,y),x1+x2= ,x=
,x= ,垂直平分线NG的方程为y-y=-
,垂直平分线NG的方程为y-y=- ,由此能求出点G横坐标的取值范围.
,由此能求出点G横坐标的取值范围.解答:解:(Ⅰ)由题意可知:c=1,a2=b2-c2,e=
 …(2分)
…(2分)解得:a=
 ,b=1(3分)
,b=1(3分)故椭圆的方程为:
 =1(4分)
=1(4分)(II)设直线AB的方程为y=k(x+1)(k≠0),(5分)
联立,得
 ,
,整理得(1+2k2)x2+4k2x+2k2-2=0(7分)
∵直线AB过椭圆的左焦点F∴方程有两个不等实根.(8分)
记A(x1,y1),B(x2,y2),AB的中点N(x,y)
则x1+x2=
 (9分)
(9分)x=
 (10分)
(10分)垂直平分线NG的方程为y-y=-
 ,(11分)
,(11分)令y=0,得xG=x+ky=-

=-
 .(12分)
.(12分)∵k≠0,∴-
 <0(13分)
<0(13分)∴点G横坐标的取值范围为(-
 ,0).(14分)
,0).(14分)点评:本题主要考查直线与圆锥曲线的综合应用能力,综合性强,是高考的重点,易错点是知识体系不牢固.本题具体涉及到轨迹方程的求法及直线与椭圆的相关知识,解题时要注意合理地进行等价转化.

练习册系列答案
相关题目
 的左焦点F及点A(0,b),原点O到直线FA的距离为
的左焦点F及点A(0,b),原点O到直线FA的距离为 b.
b. 的左焦点为F(﹣1,0),离心率为
的左焦点为F(﹣1,0),离心率为 ,过点F的直线l与椭圆C交于A、B两点.
,过点F的直线l与椭圆C交于A、B两点. 的左焦点为F(-1,0),离心率为
的左焦点为F(-1,0),离心率为 ,过点F的直线l与椭圆C交于A、B两点.
,过点F的直线l与椭圆C交于A、B两点. 的左焦点F,C与过原点的直线相交于A,B两点,连结AF,BF,若|AB|=10,|AF|=6,
的左焦点F,C与过原点的直线相交于A,B两点,连结AF,BF,若|AB|=10,|AF|=6, ,则C的离心率为( )
,则C的离心率为( )


