题目内容
已知椭圆C: 的左焦点F,C与过原点的直线相交于A,B两点,连结AF,BF,若|AB|=10,|AF|=6,
的左焦点F,C与过原点的直线相交于A,B两点,连结AF,BF,若|AB|=10,|AF|=6, ,则C的离心率为( )
,则C的离心率为( )A.

B.

C.

D.

【答案】分析:在△AFB中,由余弦定理可得|AF|2=|AB|2+|BF|2-2|AB||BF|cos∠ABF,即可得到|BF|,设F′为椭圆的右焦点,连接BF′,AF′.根据对称性可得四边形AFBF′是矩形.
即可得到a,c,进而取得离心率.
解答:解:如图所示,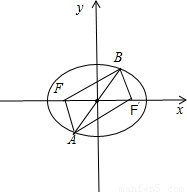 在△AFB中,由余弦定理可得|AF|2=|AB|2+|BF|2-2|AB||BF|cos∠ABF,
在△AFB中,由余弦定理可得|AF|2=|AB|2+|BF|2-2|AB||BF|cos∠ABF,
∴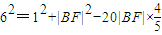 ,化为(|BF|-8)2=0,解得|BF|=8.
,化为(|BF|-8)2=0,解得|BF|=8.
设F′为椭圆的右焦点,连接BF′,AF′.根据对称性可得四边形AFBF′是矩形.
∴|BF′|=6,|FF′|=10.
∴2a=8+6,2c=10,解得a=7,c=5.
∴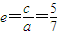 .
.
故选B.
点评:熟练掌握余弦定理、椭圆的定义、对称性、离心率、矩形的性质等基础知识是解题的关键.
即可得到a,c,进而取得离心率.
解答:解:如图所示,
 在△AFB中,由余弦定理可得|AF|2=|AB|2+|BF|2-2|AB||BF|cos∠ABF,
在△AFB中,由余弦定理可得|AF|2=|AB|2+|BF|2-2|AB||BF|cos∠ABF,∴
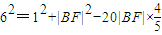 ,化为(|BF|-8)2=0,解得|BF|=8.
,化为(|BF|-8)2=0,解得|BF|=8.设F′为椭圆的右焦点,连接BF′,AF′.根据对称性可得四边形AFBF′是矩形.
∴|BF′|=6,|FF′|=10.
∴2a=8+6,2c=10,解得a=7,c=5.
∴
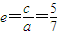 .
.故选B.
点评:熟练掌握余弦定理、椭圆的定义、对称性、离心率、矩形的性质等基础知识是解题的关键.

练习册系列答案
相关题目
 的左焦点F及点A(0,b),原点O到直线FA的距离为
的左焦点F及点A(0,b),原点O到直线FA的距离为 b.
b. 的左焦点为F(﹣1,0),离心率为
的左焦点为F(﹣1,0),离心率为 ,过点F的直线l与椭圆C交于A、B两点.
,过点F的直线l与椭圆C交于A、B两点. 的左焦点为F(-1,0),离心率为
的左焦点为F(-1,0),离心率为 ,过点F的直线l与椭圆C交于A、B两点.
,过点F的直线l与椭圆C交于A、B两点.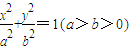 的左焦点为F(-1,0),离心率为
的左焦点为F(-1,0),离心率为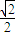 ,过点F的直线l与椭圆C交于A、B两点.
,过点F的直线l与椭圆C交于A、B两点.