题目内容
已知椭圆C：
的左焦点为F（﹣1，0），离心率为
，过点F的直线l与椭圆C交于A、B两点．
（Ⅰ）求椭圆C的方程；
（Ⅱ）设过点F不与坐标轴垂直的直线交椭圆C于A、B两点，线段AB的垂直平分线与x轴交于点G，求点G横坐标的取值范围．
的左焦点为F（﹣1，0），离心率为，过点F的直线l与椭圆C交于A、B两点．（Ⅰ）求椭圆C的方程；
（Ⅱ）设过点F不与坐标轴垂直的直线交椭圆C于A、B两点，线段AB的垂直平分线与x轴交于点G，求点G横坐标的取值范围．
解：（Ⅰ）由题意可知：c=1，a2=b2﹣c2，e=
解得：a=
，b=1
故椭圆的方程为：
=1
（II）设直线AB的方程为y=k（x+1）（k≠0），
联立，得
，整理得（1+2k2）x2+4k2x+2k2﹣2=0
∵直线AB过椭圆的左焦点F
∴方程有两个不等实根．
记A（x1，y1），B（x2，y2），AB的中点N（x0，y0）
则x1+x2=
，x0=
垂直平分线NG的方程为y﹣y0=﹣
，
令y=0，得xG=x0+ky0=﹣
=﹣
．
∵k≠0，∴﹣
＜0
∴点G横坐标的取值范围为（﹣
，0）．
解得：a=，b=1故椭圆的方程为：
=1（II）设直线AB的方程为y=k（x+1）（k≠0），
联立，得
，整理得（1+2k2）x2+4k2x+2k2﹣2=0∵直线AB过椭圆的左焦点F
∴方程有两个不等实根．
记A（x1，y1），B（x2，y2），AB的中点N（x0，y0）
则x1+x2=
，x0=垂直平分线NG的方程为y﹣y0=﹣
，令y=0，得xG=x0+ky0=﹣
=﹣．∵k≠0，∴﹣
＜0∴点G横坐标的取值范围为（﹣
，0）．
练习册系列答案
小夫子全能检测系列答案
相关题目
的左焦点F及点A（0，b），原点O到直线FA的距离为
b．
的左焦点为F（-1，0），离心率为
，过点F的直线l与椭圆C交于A、B两点．
的左焦点F，C与过原点的直线相交于A，B两点，连结AF，BF，若|AB|=10，|AF|=6，
，则C的离心率为（ ）
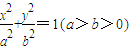的左焦点为F（-1，0），离心率为
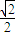，过点F的直线l与椭圆C交于A、B两点．