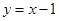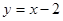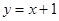题目内容
(本小题满分14分)已知函数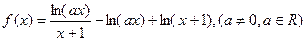 .
.
(Ⅰ)求函数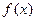 的定义域;
的定义域;
(Ⅱ)求函数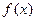 的单调区间;
的单调区间;
(Ⅲ)当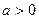 时,若存
时,若存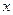 在使得
在使得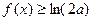 成立,求
成立,求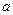 的取值范围.
的取值范围.
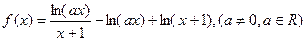 .
.(Ⅰ)求函数
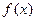 的定义域;
的定义域;(Ⅱ)求函数
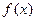 的单调区间;
的单调区间;(Ⅲ)当
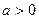 时,若存
时,若存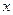 在使得
在使得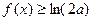 成立,求
成立,求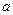 的取值范围.
的取值范围.
(本题满分14分)
解:(Ⅰ)当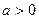 时,由
时,由 得
得 ;当
;当 时由
时由 得
得
综上:当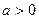 时函数
时函数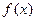 的定义域为
的定义域为 ;
;
当 时函数
时函数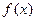 的定义域为
的定义域为 ………3分
………3分
(Ⅱ)


 ………5分
………5分
令 时,得
时,得 即
即 ,
,
①当 时,
时, 时
时 ,当
,当 时,
时, ,
,
故当 时,函数的递增区间为
时,函数的递增区间为 ,递减区间为
,递减区间为
②当 时,
时, ,所以
,所以 ,
,
故当 时,
时,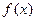 在
在 上单调
上单调 递增.
递增.
③当 时,若
时,若 ,
, ;若
;若 ,
, ,
,
故当 时,
时,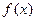 的单调递增区间为
的单调递增区间为 ;单调递减区间为
;单调递减区间为 .
.
综上:当 时,
时,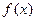 的单调递增区间为
的单调递增区间为 ;单调递减区间为
;单调递减区间为
当 时,
时,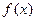 的单调递增区间为
的单调递增区间为 ;
;
当 时,
时,
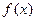 的单调递增区间为
的单调递增区间为 ;单调递减区间为
;单调递减区间为 ;
;
…………10分
(Ⅲ)因为当 时,函数的递增区间为
时,函数的递增区间为 ;单调递减区间为
;单调递减区间为
若存在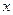 使得
使得 成立,只须
成立,只须 ,
,
即 ≥
≥ ≥
≥
 <
<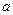 ≤1…………14分
≤1…………14分
解:(Ⅰ)当
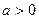 时,由
时,由 得
得 ;当
;当 时由
时由 得
得
综上:当
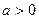 时函数
时函数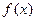 的定义域为
的定义域为 ;
; 当
 时函数
时函数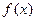 的定义域为
的定义域为 ………3分
………3分(Ⅱ)


 ………5分
………5分令
 时,得
时,得 即
即 ,
,①当
 时,
时, 时
时 ,当
,当 时,
时, ,
,故当
 时,函数的递增区间为
时,函数的递增区间为 ,递减区间为
,递减区间为
②当
 时,
时, ,所以
,所以 ,
,故当
 时,
时,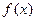 在
在 上单调
上单调 递增.
递增.③当
 时,若
时,若 ,
, ;若
;若 ,
, ,
,故当
 时,
时,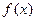 的单调递增区间为
的单调递增区间为 ;单调递减区间为
;单调递减区间为 .
.综上:当
 时,
时,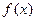 的单调递增区间为
的单调递增区间为 ;单调递减区间为
;单调递减区间为
当
 时,
时,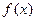 的单调递增区间为
的单调递增区间为 ;
;当
 时,
时,
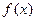 的单调递增区间为
的单调递增区间为 ;单调递减区间为
;单调递减区间为 ;
; …………10分
(Ⅲ)因为当
 时,函数的递增区间为
时,函数的递增区间为 ;单调递减区间为
;单调递减区间为
若存在
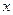 使得
使得 成立,只须
成立,只须 ,
,
|
 ≥
≥ ≥
≥
 <
<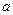 ≤1…………14分
≤1…………14分 略

练习册系列答案
 步步高达标卷系列答案
步步高达标卷系列答案
相关题目
 ≤
≤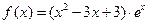 定义域为
定义域为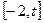 (
(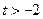 ),设
),设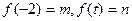 .
.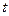 的取值范围,使得函数
的取值范围,使得函数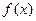 在
在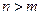 ;
;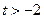 ,总存在
,总存在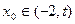 ,满足
,满足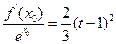 ,并确定这样的
,并确定这样的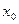 的个数.
的个数.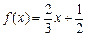 ,
,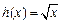 .
.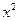 [h(x)]
[h(x)]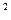 ,求F(x)的单调区间与极值;
,求F(x)的单调区间与极值;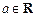 ,解关于x的方程
,解关于x的方程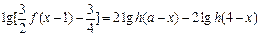 ;
;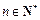 ,证明:
,证明: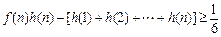 .
. 时,f
时,f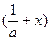 >f
>f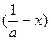 ;
;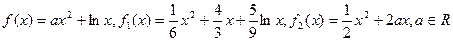 .
.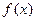 在点
在点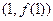 处的切线方程;
处的切线方程;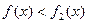 在区间
在区间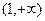 上恒成立,求
上恒成立,求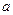 的取值范围;
的取值范围;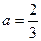 时,求证:在区间
时,求证:在区间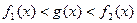 恒成立的函数
恒成立的函数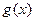 有无穷多个.
有无穷多个.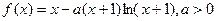 .
.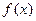 的单调区间;
的单调区间;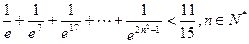 .
.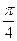 .
. ?若存在,求出最小的正整数k,否则请说明理由.
?若存在,求出最小的正整数k,否则请说明理由.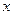 的函数
的函数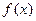 与数列
与数列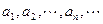 具有关系:
具有关系: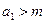 ,
,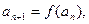 (
(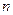 =1,2,3,…)(
=1,2,3,…)(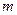 为常数),又设函数
为常数),又设函数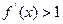 ,
,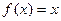 的实根.
的实根.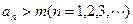 ;
;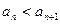 .
.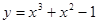 在点P(-1,-1)处的切线方程是 ( )
在点P(-1,-1)处的切线方程是 ( )