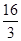题目内容
(理数)(14分) 已知函数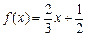 ,
,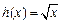 .
.
(Ⅰ)设函数F(x)=18f(x)-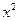 [h(x)]
[h(x)]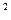 ,求F(x)的单调区间与极值;
,求F(x)的单调区间与极值;
(Ⅱ)设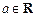 ,解关于x的方程
,解关于x的方程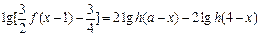 ;
;
(Ⅲ)设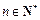 ,证明:
,证明: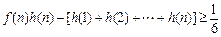 .
.
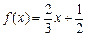 ,
,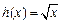 .
.(Ⅰ)设函数F(x)=18f(x)-
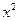 [h(x)]
[h(x)]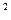 ,求F(x)的单调区间与极值;
,求F(x)的单调区间与极值;(Ⅱ)设
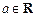 ,解关于x的方程
,解关于x的方程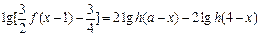 ;
;(Ⅲ)设
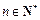 ,证明:
,证明: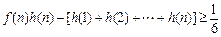 .
.(理数) 解:(Ⅰ)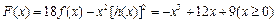 ,
,
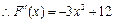 .
.
令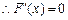 ,得
,得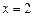 (
(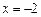 舍去).
舍去).
当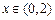 时.
时.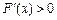 ;当
;当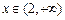 时,
时,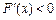 ,
,
故当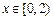 时,
时,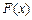 为增函数;当
为增函数;当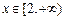 时,
时,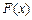 为减函数.
为减函数.
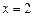 为
为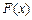 的极大值点,且
的极大值点,且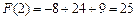 .………………………………4分
.………………………………4分
(Ⅱ)原方程可化为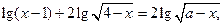 ,即
,即
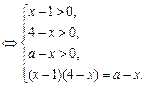
 ……………6分
……………6分
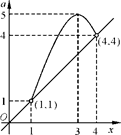
①当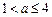 时,原方程有一解
时,原方程有一解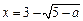 ;
;
②当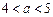 时,原方程有二解
时,原方程有二解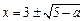 ;…………8分
;…………8分
③当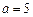 时,原方程有一解
时,原方程有一解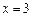 ;
;
④当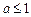 或
或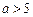 时,原方程无解.……………………10分
时,原方程无解.……………………10分
(Ⅲ)由已知得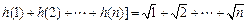 ,
,
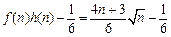 .
.
设数列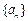 的前n项和为
的前n项和为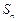 ,且
,且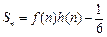 (
(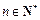 )
)
从而有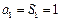 ,当
,当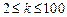 时,
时,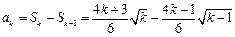 .
.
又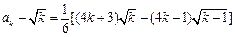
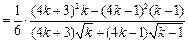
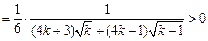 .
.
即对任意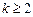 时,有
时,有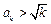 ,又因为
,又因为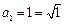 ,所以
,所以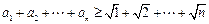 ………14分.
………14分.
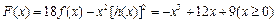 ,
,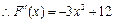 .
.令
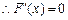 ,得
,得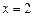 (
(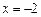 舍去).
舍去).当
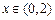 时.
时.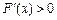 ;当
;当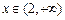 时,
时,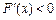 ,
,故当
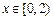 时,
时,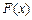 为增函数;当
为增函数;当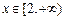 时,
时,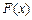 为减函数.
为减函数.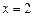 为
为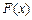 的极大值点,且
的极大值点,且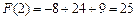 .………………………………4分
.………………………………4分(Ⅱ)原方程可化为
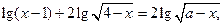 ,即
,即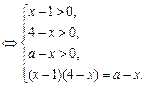
 ……………6分
……………6分
①当
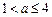 时,原方程有一解
时,原方程有一解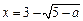 ;
;②当
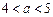 时,原方程有二解
时,原方程有二解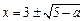 ;…………8分
;…………8分③当
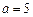 时,原方程有一解
时,原方程有一解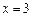 ;
;④当
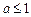 或
或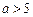 时,原方程无解.……………………10分
时,原方程无解.……………………10分(Ⅲ)由已知得
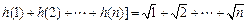 ,
,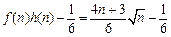 .
.设数列
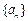 的前n项和为
的前n项和为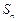 ,且
,且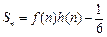 (
(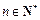 )
)从而有
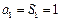 ,当
,当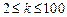 时,
时,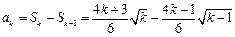 .
.又
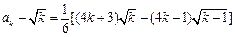
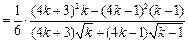
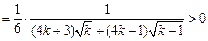 .
.即对任意
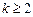 时,有
时,有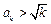 ,又因为
,又因为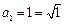 ,所以
,所以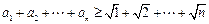 ………14分.
………14分.略

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
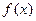 是定义在
是定义在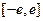 上的奇函数,当
上的奇函数,当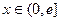 时
时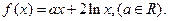
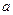 ,使得当
,使得当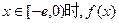 的最小值是4?如果存在,求出
的最小值是4?如果存在,求出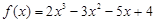 的导数
的导数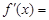 ,
,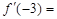
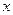 ,有
,有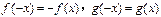 ,且
,且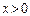 时,
时,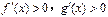 ,则
,则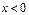 时 ( )
时 ( )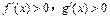
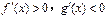
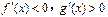
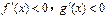
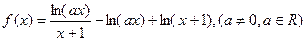 .
.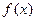 的定义域;
的定义域;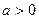 时,若存
时,若存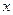 在使得
在使得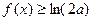 成立,求
成立,求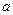 的取值范围.
的取值范围.
 在
在 与
与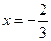 时,都取得极值。
时,都取得极值。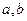 的值;
的值;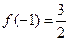 ,求
,求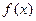 的单调区间和极值;
的单调区间和极值;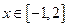 都有
都有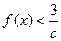 恒成立,求
恒成立,求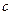 的取值范围。
的取值范围。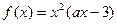 ,其中a为常数.
,其中a为常数.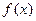 的一个极值点,求a的值;
的一个极值点,求a的值;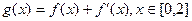 ,在x=0处取得最大值,求正数a的取值范围.
,在x=0处取得最大值,求正数a的取值范围.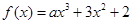 ,若
,若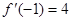 ,则
,则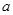 =
=