题目内容
20.四面体ABCD的四个顶点都在球O的球面上,AB=4,BC=CD=2,∠BCD=120°,AB⊥平面BCD,则球O的表面积为32π.分析 取CD的中点E,连结AE,BE,作出外接球的球心,求出半径,即可求出表面积.
解答 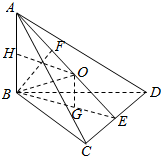 解:取CD的中点E,连结AE,BE,
解:取CD的中点E,连结AE,BE,
∵在四面体ABCD中,AB⊥平面BCD,BC=CD,
△BCD的外心为G,作OG∥AB交AB的中垂线HO于O,O为外接球的中心,
∵BC=CD=2,∠BCD=120°,
∴BD=$\sqrt{4+4-2×2×2×(-\frac{1}{2})}$=2$\sqrt{3}$,
∴BG=$\frac{1}{2}$×$\frac{2\sqrt{3}}{\frac{\sqrt{3}}{2}}$=2
∴R=$\sqrt{4+4}$=2$\sqrt{2}$.
四面体ABCD外接球的表面积为:4πR2=32π.
故答案为:32π.
点评 本题考查球的内接体知识,考查空间想象能力,确定球的半径是解题的关键.

练习册系列答案
 黄冈经典趣味课堂系列答案
黄冈经典趣味课堂系列答案 启东小题作业本系列答案
启东小题作业本系列答案
相关题目
10.在平面直角坐标系xOy中,M为不等式组$\left\{\begin{array}{l}2x-y-2≥0\\ x+2y-1≥0\\ 3x+y-8≤0\end{array}\right.$,所表示的区域上一动点,则直线OM斜率的最小值为( )
| A. | $-\frac{1}{3}$ | B. | $-\frac{1}{2}$ | C. | 1 | D. | 2 |
8.若实数x,y满足$\left\{\begin{array}{l}{x-y+2≥0}\\{x+y≥0}\\{x≤3}\end{array}\right.$,则z=x-2y的最小值为( )
| A. | -7 | B. | -3 | C. | 1 | D. | 9 |
15.设x,y满足约束条件$\left\{\begin{array}{l}{x≤3}\\{x-y+5≥0}\\{x+y≥0}\end{array}\right.$,若$\overline{a}$=(y,1),$\overline{b}$=($\frac{1}{x+1}$,0),则z=$\overline{a}•\overline{b}$的取值范围是( )
| A. | [-$\frac{5}{3}$,-$\frac{3}{4}$] | B. | (-∞,-$\frac{5}{3}$] | C. | (-∞,-$\frac{5}{3}$]∩[-$\frac{3}{4}$,+∞) | D. | [-$\frac{3}{4}$,+∞) |
10.若sinα+cosα=-$\frac{7}{5}$,则角α是( )
| A. | 第一象限角 | B. | 第二象限角 | C. | 第三象限角 | D. | 第四象限角 |