题目内容
下列命题.
①“A∩B=A”成立的必要条件是“A?B”;
②“若x2+y2=0,则x,y全为0”的否命题;
③“全等三角形是相似三角形”的逆命题;
④“圆内接四边形对角互补”的逆否命题.
其中为真命题的是( )
①“A∩B=A”成立的必要条件是“A?B”;
②“若x2+y2=0,则x,y全为0”的否命题;
③“全等三角形是相似三角形”的逆命题;
④“圆内接四边形对角互补”的逆否命题.
其中为真命题的是( )
| A、①③ | B、②④ | C、④、 | D、①②④ |
考点:四种命题
专题:简易逻辑
分析:根据交集的概念,必要条件的概念,x2+y2≠0时x,y取值情况,以及相似三角形的定义,圆内接四边形对角的性质即可找出真命题.
解答:
解:①假命题,A∩B=A得到A⊆B,即A=B,或A?B,∴不一定得到A?B;
②真命题,否命题为“若x2+y2≠0,则x,y不全为0”;
③假命题,逆命题为“相似三角形是全等三角形”,三角形相似不一定全等;
④真命题,该命题为真命题,这是圆内接四边形的性质,所以它的逆否命题也是真命题;
∴为真命题的是②④.
故选B.
②真命题,否命题为“若x2+y2≠0,则x,y不全为0”;
③假命题,逆命题为“相似三角形是全等三角形”,三角形相似不一定全等;
④真命题,该命题为真命题,这是圆内接四边形的性质,所以它的逆否命题也是真命题;
∴为真命题的是②④.
故选B.
点评:考查交集的概念,必要条件的概念,以及否命题、逆命题、逆否命题的概念,三角形相似与全等的关系,圆内接四边形的对角的性质.

练习册系列答案
 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案 周周清检测系列答案
周周清检测系列答案 轻巧夺冠周测月考直通高考系列答案
轻巧夺冠周测月考直通高考系列答案
相关题目
已知函数f(x)=
sin2x+cos2x,若f(x-φ)为偶函数,则φ的一个值为( )
| 3 |
A、
| ||
B、
| ||
C、
| ||
D、
|
与函数y=x相等的函数是( )
A、y=(
| |||
B、y=
| |||
C、y=
| |||
D、y=
|
如图所示程序框图中,某班50名学生,在一次数学考试中,an表示学号为n的学生的成绩,则( )
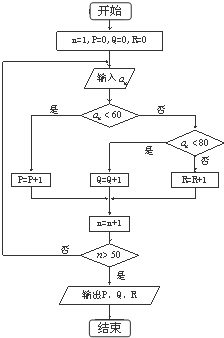

| A、P表示成绩不高于60分的人数 |
| B、Q表示成绩低于80分的人数 |
| C、R表示成绩高于80分的人数 |
| D、Q表示成绩不低于60分,且低于80分人数 |
设函数f(x)=(x2-8x+c1)(x2-8x+c2)(x2-8x+c3) (x2-8x+c4),集合M={x|f(x)=0}={x1,x2…,x7}⊆N+,设c1≥c2≥c3≥c4,则c1-c4( )
| A、9 | B、8 | C、7 | D、6 |
若a是R中的元素,但不是Q中的元素,则a可以是 ( )
| A、3.14 | ||||
| B、log48 | ||||
| C、-5 | ||||
D、
|
若xy≠0,则等式
=-4xy
成立的条件是( )
| 16x2y3 |
| y |
| A、x>0,y>0 |
| B、x>0,y<0 |
| C、x<0,y>0 |
| D、x<0,y<0 |