题目内容
设函数
，的导函数为
，且
，
，则下列不等式成立的是（注：e为自然对数的底数）（ ）
A． | B． |
C． | D． |
B
解析试题分析：设g(x)=e
f（x）∴g'(x)="-" ef（x）+ ef
（x）= e（f（x）－f(x)）<0
所以g(x)为减函数.∵g(0)=e0f(0)=" f(0)" ,g(-1)=
, 
,
且g(2)>g(0)>g(－1),∴
< f(0)< 
，故选B.
考点：1.求导数；2.函数的单调性.
练习册系列答案
名校练考卷期末冲刺卷系列答案
相关题目
已知曲线方程
，若对任意实数
，直线
都不是曲线
)的切线，则的取值范围是（ ）
A． | B． |
C． | D． 且 |
设
，若f(3)="3f" ′(x0)，则x0＝（ ）
| A．±1 | B．±2 | C．± | D．2 |
函数
为自然对数的底数）的值域是实数集R，则实数a的取值范围是（ ）
A． | B． | C． | D．[0，1] |
设直线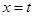
与函数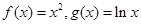
的图象分别交于点
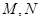，则当
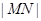达到最小时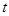
的值为( )
| A．1 | B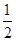． | C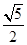． | D． |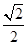
若过点
的直线与曲线
和
都相切，则
的值为 （ ）
| A．2 | B． | C．2或 | D．3或 |
对于实数集
上的可导函数
，若满足
，则在区间[1,2]上必有（ ）
A． |
B． |
C． |
| D．或 |
已知函数
则下列结论正确的（ ）
A． 在 上恰有一个零点 |
| B．在上恰有两个零点 |
C．在 上恰有一个零点 |
| D．在上恰有两个零点 |
若曲线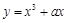
在坐标原点处的切线方程是
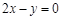，则实数
（ ）
| A．1 | B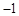． | C．2 | D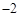． |