题目内容
已知函数 则下列结论正确的( )
则下列结论正确的( )
A. 在 在 上恰有一个零点 上恰有一个零点 |
B. 在 在 上恰有两个零点 上恰有两个零点 |
C. 在 在 上恰有一个零点 上恰有一个零点 |
D. 在 在 上恰有两个零点 上恰有两个零点 |
C
解析试题分析:根据函数零点存在定理, ,所以,A,B错误。
,所以,A,B错误。
因为, ,
,
所以, ,在
,在 ,
, ,
,
即 是增函数,所以,
是增函数,所以, 在
在 上恰有一个零点。故选C。
上恰有一个零点。故选C。
考点:函数的零点存在定理,应用导数研究函数的单调性。
点评:中档题,通过研究函数的单调性及函数零点存在定理,明确函数零点的个数

练习册系列答案
相关题目
曲线y= 在点(2,4)处的切线与坐标轴围成的三角形面积为( )
在点(2,4)处的切线与坐标轴围成的三角形面积为( )
| A.1 | B.2 | C. | D. |
设函数 ,的导函数为
,的导函数为 ,且
,且 ,
, ,则下列不等式成立的是(注:e为自然对数的底数)( )
,则下列不等式成立的是(注:e为自然对数的底数)( )
A. | B. |
C. | D. |
设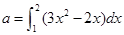 ,则二项式
,则二项式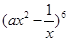 展开式中的第四项为( )
展开式中的第四项为( )
A.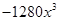 | B.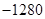 | C. | D.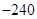 |
已知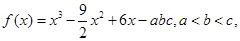 且
且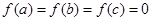 ,现给出如下结论:
,现给出如下结论:
①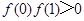 ;②
;②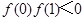 ;③
;③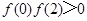 ;④
;④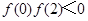 .其中正确结论的序号为:( )
.其中正确结论的序号为:( )
| A.①③ | B.①④ | C.②④ | D.②③ |
设曲线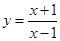 在点
在点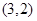 处的切线与直线
处的切线与直线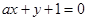 垂直,则
垂直,则 等于 ( )
等于 ( )
A.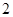 | B. | C. | D.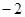 |
函数f(x)= +
+ -3x—4在[0,2]上的最小值是
-3x—4在[0,2]上的最小值是
A.— | B.—  | C.-4 | D.—1 |
已知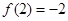 ,
,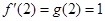 ,
, ,则函数
,则函数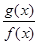 在
在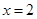 处的导数值为( )
处的导数值为( )
A.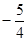 | B.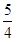 | C. | D. |
设函数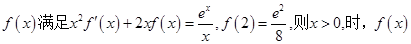 ( )
( )
| A.有极大值,无极小值 | B.有极小值,无极大值 |
| C.既有极大值又有极小值 | D.既无极大值也无极小值 |