题目内容
椭圆mx2+y2=1的离心率是
,则它的长轴长是( )
| ||
| 2 |
| A、1 | B、1或2 | C、2 | D、2或4 |
考点:椭圆的简单性质
专题:圆锥曲线的定义、性质与方程
分析:首先把椭圆的方程变成标准形式,进一步根据焦点所在的位置进行分类讨论,以离心率为等量建立方程进一步求得结果.
解答:
解:把椭圆mx2+y2=1方程转化为:
+y2=1
分两种情况:①
>1
椭圆的离心率
则:
=
解得:m=
进一步得长轴长为4
②
<1
椭圆的离心率
则:长轴长为2
故选:D
| x2 | ||
|
分两种情况:①
| 1 |
| m |
椭圆的离心率
| ||
| 2 |
| ||
|
| 3 |
| 4 |
| 1 |
| 4 |
②
| 1 |
| m |
椭圆的离心率
| ||
| 2 |
故选:D
点评:本题考查的知识点:椭圆的标准方程,椭圆中a、b、c的关系,椭圆的离心率,及分类讨论思想.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
直线y=1-x交抛物线y2=2px(p>0)于M,N两点,且|
+
|=|
-
|,则p的值为( )
| OM |
| ON |
| OM |
| ON |
| A、2 | ||
| B、1 | ||
C、
| ||
D、
|
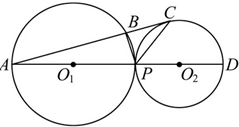 如图,⊙O1和⊙O2外切于点P,延长PO1交⊙O1于点A,延长PO2交⊙O2于点D,若AC与⊙O2相切于点C,且交⊙O1于点B.求证:
如图,⊙O1和⊙O2外切于点P,延长PO1交⊙O1于点A,延长PO2交⊙O2于点D,若AC与⊙O2相切于点C,且交⊙O1于点B.求证: