题目内容
对于函数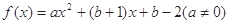 ,若存在实数
,若存在实数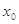 ,使
,使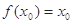 成立,则称
成立,则称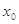 为
为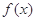 的不动点.
的不动点.
⑴当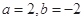 时,求
时,求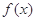 的不动点;
的不动点;
⑵若对于任何实数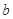 ,函数
,函数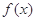 恒有两相异的不动点,求实数
恒有两相异的不动点,求实数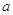 的取值范围;
的取值范围;
⑶在⑵的条件下,若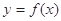 的图象上A、B两点的横坐标是函数
的图象上A、B两点的横坐标是函数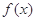 的不动点,且直线
的不动点,且直线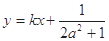 是线段AB的垂直平分线,求实数b的取值范围.
是线段AB的垂直平分线,求实数b的取值范围.
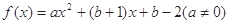 ,若存在实数
,若存在实数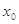 ,使
,使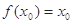 成立,则称
成立,则称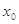 为
为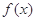 的不动点.
的不动点.⑴当
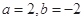 时,求
时,求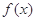 的不动点;
的不动点;⑵若对于任何实数
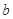 ,函数
,函数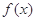 恒有两相异的不动点,求实数
恒有两相异的不动点,求实数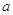 的取值范围;
的取值范围;⑶在⑵的条件下,若
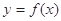 的图象上A、B两点的横坐标是函数
的图象上A、B两点的横坐标是函数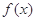 的不动点,且直线
的不动点,且直线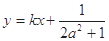 是线段AB的垂直平分线,求实数b的取值范围.
是线段AB的垂直平分线,求实数b的取值范围.
(1)
 的不动点是-1,2.
的不动点是-1,2.(2)
 (3)0>
(3)0>
(1)设x为不动点,则有2x2-x-4=x,变形为2x2-2x-4=0,解方程即可.
(2)将f(x)=x转化为ax2+bx+b-2=0.由已知,此方程有相异二实根,则有△x>0恒成立求解;
(3)由垂直平分线的定义解决,由A、B两点的横坐标是函数f(x)的不动点,则有kAB=1,再由直线 是线段AB的垂直平分线,得到k=-1,再由中点在直线
是线段AB的垂直平分线,得到k=-1,再由中点在直线 上求解.
上求解.
(2)将f(x)=x转化为ax2+bx+b-2=0.由已知,此方程有相异二实根,则有△x>0恒成立求解;
(3)由垂直平分线的定义解决,由A、B两点的横坐标是函数f(x)的不动点,则有kAB=1,再由直线
 是线段AB的垂直平分线,得到k=-1,再由中点在直线
是线段AB的垂直平分线,得到k=-1,再由中点在直线 上求解.
上求解.
练习册系列答案
相关题目
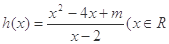 ,且
,且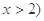 ,函数
,函数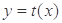 的图象经过点
的图象经过点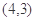 ,且
,且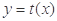 与
与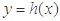 的图象关于直线
的图象关于直线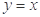 对称,将函数
对称,将函数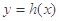 的图象向左平移2个单位后得到函数
的图象向左平移2个单位后得到函数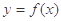 的图象.
的图象.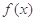 的解析式;
的解析式;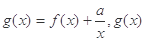 在区间
在区间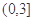 上的值不小于8,求实数
上的值不小于8,求实数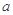 的取值范围.
的取值范围.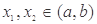 (其中
(其中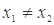 ),有
),有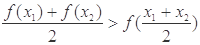 ,称函数
,称函数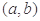 的图象是“下凸的”.判断此题中的函数
的图象是“下凸的”.判断此题中的函数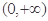 是否是“下凸的”?如果是,给出证明;如果不是,说明理由.
是否是“下凸的”?如果是,给出证明;如果不是,说明理由.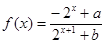 (
(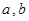 为实常数).
为实常数).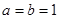 时,证明:
时,证明: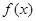 不是奇函数;
不是奇函数;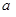 与
与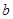 的值;
的值;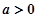 时,若对任意的
时,若对任意的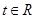 ,不等式
,不等式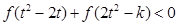
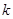 的取值范围.
的取值范围.  在
在 上是减函数,则实数
上是减函数,则实数 的取值范围是___.
的取值范围是___.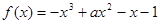 在
在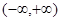 上是单调函数,则实数
上是单调函数,则实数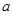 的取值范围是( )
的取值范围是( )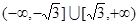
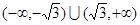
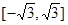
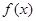 满足
满足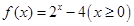 ,则
,则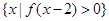 =_____________
=_____________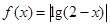 ,在其上为增函数的是( )
,在其上为增函数的是( )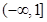
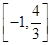
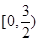
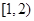
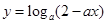 在[0,1]上单调递减,则实数a的取值范围是_________.
在[0,1]上单调递减,则实数a的取值范围是_________.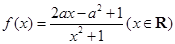 ,其中
,其中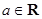 .
.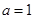 时,求曲线
时,求曲线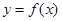 在点
在点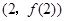 处的切线方程;
处的切线方程;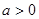 时,求函数
时,求函数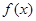 的单调区间与极值.
的单调区间与极值.