题目内容
已知函数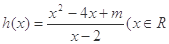 ,且
,且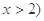 ,函数
,函数 的图象经过点
的图象经过点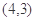 ,且
,且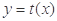 与
与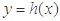 的图象关于直线
的图象关于直线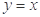 对称,将函数
对称,将函数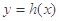 的图象向左平移2个单位后得到函数
的图象向左平移2个单位后得到函数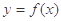 的图象.
的图象.
(Ⅰ)求函数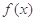 的解析式;
的解析式;
(Ⅱ)若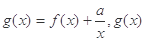 在区间
在区间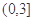 上的值不小于8,求实数
上的值不小于8,求实数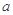 的取值范围.
的取值范围.
(III)若函数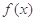 满足:对任意的
满足:对任意的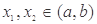 (其中
(其中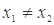 ),有
),有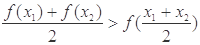 ,称函数
,称函数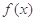 在
在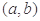 的图象是“下凸的”.判断此题中的函数
的图象是“下凸的”.判断此题中的函数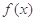 图象在
图象在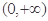 是否是“下凸的”?如果是,给出证明;如果不是,说明理由.
是否是“下凸的”?如果是,给出证明;如果不是,说明理由.
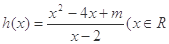 ,且
,且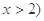 ,函数
,函数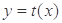 的图象经过点
的图象经过点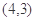 ,且
,且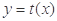 与
与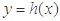 的图象关于直线
的图象关于直线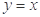 对称,将函数
对称,将函数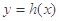 的图象向左平移2个单位后得到函数
的图象向左平移2个单位后得到函数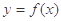 的图象.
的图象.(Ⅰ)求函数
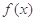 的解析式;
的解析式;(Ⅱ)若
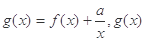 在区间
在区间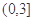 上的值不小于8,求实数
上的值不小于8,求实数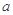 的取值范围.
的取值范围.(III)若函数
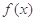 满足:对任意的
满足:对任意的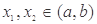 (其中
(其中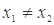 ),有
),有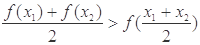 ,称函数
,称函数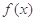 在
在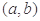 的图象是“下凸的”.判断此题中的函数
的图象是“下凸的”.判断此题中的函数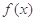 图象在
图象在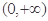 是否是“下凸的”?如果是,给出证明;如果不是,说明理由.
是否是“下凸的”?如果是,给出证明;如果不是,说明理由..(Ⅰ)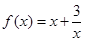 (Ⅱ)a≥12(III)是
(Ⅱ)a≥12(III)是
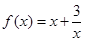 (Ⅱ)a≥12(III)是
(Ⅱ)a≥12(III)是本试题主要考查了函数的解析式和函数的单调性和函数的下凸形的运用。
(1)由题意得h(x)的图象经过(3,4),
代入得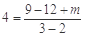 ,解得m="7." ∴
,解得m="7." ∴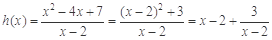 分
分
∴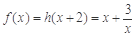 .
.
(2)∵ ,
,
∴ 由已知有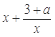 ≥8有a≥-x2+8x-3, 令t(x)=-x2+8x-3,则t(x)=-(x-4)2+13,于是t(x)在(0,3)上是增函数.∴ t(x)max=12.∴ a≥12
≥8有a≥-x2+8x-3, 令t(x)=-x2+8x-3,则t(x)=-(x-4)2+13,于是t(x)在(0,3)上是增函数.∴ t(x)max=12.∴ a≥12
(3) 的图象在
的图象在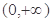 是“下凸的”,根据新定义证明,
是“下凸的”,根据新定义证明,
解:(Ⅰ)由题意得h(x)的图象经过(3,4),
代入得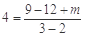 ,解得m=7. 1分
,解得m=7. 1分
∴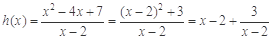 2分
2分
∴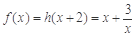 . 4分
. 4分
(Ⅱ)∵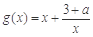 ,
,
∴ 由已知有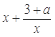 ≥8有a≥-x2+8x-3, 6分
≥8有a≥-x2+8x-3, 6分
令t(x)=-x2+8x-3,则t(x)=-(x-4)2+13,于是t(x)在(0,3)上是增函数.
∴ t(x)max=12.
∴ a≥12. 8分
(III) 的图象在
的图象在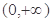 是“下凸的”. 9分
是“下凸的”. 9分
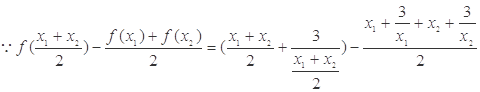

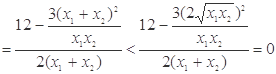

 的图象在
的图象在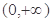 是“下凸的”. 12分
是“下凸的”. 12分
(1)由题意得h(x)的图象经过(3,4),
代入得
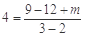 ,解得m="7." ∴
,解得m="7." ∴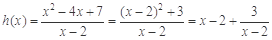 分
分∴
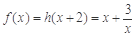 .
.(2)∵
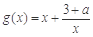 ,
,∴ 由已知有
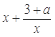 ≥8有a≥-x2+8x-3, 令t(x)=-x2+8x-3,则t(x)=-(x-4)2+13,于是t(x)在(0,3)上是增函数.∴ t(x)max=12.∴ a≥12
≥8有a≥-x2+8x-3, 令t(x)=-x2+8x-3,则t(x)=-(x-4)2+13,于是t(x)在(0,3)上是增函数.∴ t(x)max=12.∴ a≥12(3)
 的图象在
的图象在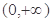 是“下凸的”,根据新定义证明,
是“下凸的”,根据新定义证明,解:(Ⅰ)由题意得h(x)的图象经过(3,4),
代入得
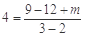 ,解得m=7. 1分
,解得m=7. 1分∴
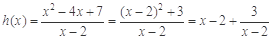 2分
2分∴
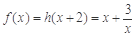 . 4分
. 4分(Ⅱ)∵
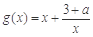 ,
,∴ 由已知有
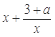 ≥8有a≥-x2+8x-3, 6分
≥8有a≥-x2+8x-3, 6分令t(x)=-x2+8x-3,则t(x)=-(x-4)2+13,于是t(x)在(0,3)上是增函数.
∴ t(x)max=12.
∴ a≥12. 8分
(III)
 的图象在
的图象在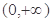 是“下凸的”. 9分
是“下凸的”. 9分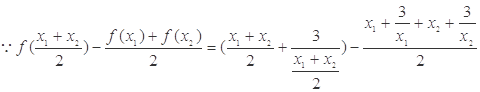

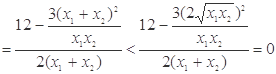

 的图象在
的图象在 是“下凸的”. 12分
是“下凸的”. 12分
练习册系列答案
 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案
相关题目
 ,设
,设 取
取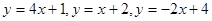 三个函数中的最小值,用分段函数写出
三个函数中的最小值,用分段函数写出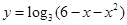 的单调减区间为 ( )
的单调减区间为 ( )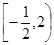
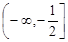

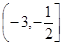
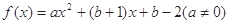 ,若存在实数
,若存在实数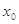 ,使
,使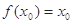 成立,则称
成立,则称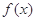 的不动点.
的不动点.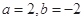 时,求
时,求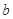 ,函数
,函数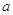 的取值范围;
的取值范围;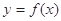 的图象上A、B两点的横坐标是函数
的图象上A、B两点的横坐标是函数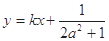 是线段AB的垂直平分线,求实数b的取值范围.
是线段AB的垂直平分线,求实数b的取值范围.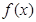 满足
满足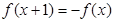 ,且在[-1,0]上单调递增,
,且在[-1,0]上单调递增,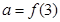 ,
,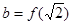 ,
,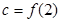 ,则
,则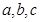 从大到小的排列顺序是 .
从大到小的排列顺序是 .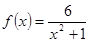
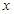 的不等式
的不等式 的解集一切实数,求实数
的解集一切实数,求实数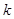 的取值范围;
的取值范围;
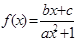 (
(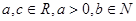 )是奇函数,
)是奇函数,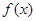 有最大值
有最大值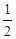
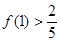 .
. 与
与 的图象交于P、Q两点,并且使得
的图象交于P、Q两点,并且使得 、
、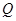 两点关于点
两点关于点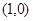 对称,若存在,求出直线
对称,若存在,求出直线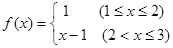 ,
,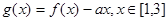 ,其中
,其中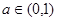 ,记函数
,记函数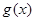 的最大值与最小值的差为
的最大值与最小值的差为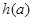 ,则
,则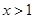 ,则函数
,则函数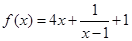 的最小值是( )
的最小值是( )