题目内容
已知函数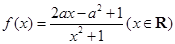 ,其中
,其中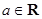 .
.
(Ⅰ)当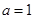 时,求曲线
时,求曲线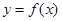 在点
在点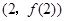 处的切线方程;
处的切线方程;
(Ⅱ)当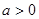 时,求函数
时,求函数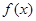 的单调区间与极值.
的单调区间与极值.
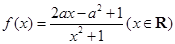 ,其中
,其中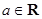 .
.(Ⅰ)当
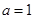 时,求曲线
时,求曲线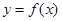 在点
在点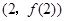 处的切线方程;
处的切线方程;(Ⅱ)当
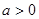 时,求函数
时,求函数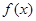 的单调区间与极值.
的单调区间与极值.(Ⅰ)
(Ⅱ)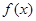 在区间
在区间 ,
, 内为减函数,在区间
内为减函数,在区间 内为增函数
内为增函数
函数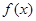 在
在 处取得极小值
处取得极小值
函数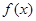 在
在 处取得极大值
处取得极大值 ,且
,且

(Ⅱ)
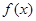 在区间
在区间 ,
, 内为减函数,在区间
内为减函数,在区间 内为增函数
内为增函数函数
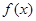 在
在 处取得极小值
处取得极小值
函数
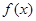 在
在 处取得极大值
处取得极大值 ,且
,且
本试题主要是考查导数的几何意义的运用以及导数求解函数的单调区间的极值的综合运用。
(1)当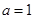 时,
时, ,
, ,
,
又 ,
, 从而点斜式得到结论。
从而点斜式得到结论。
(2)当 时,令
时,令 ,得到
,得到 ,
, 然后研究给定区间的单调性质得到极值。
然后研究给定区间的单调性质得到极值。
(Ⅰ)解:当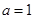 时,
时, ,
, ,
,
又 ,
, .
.
所以,曲线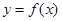 在点
在点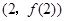 处的切线方程为
处的切线方程为 ,
,
即 。 -----------4分
。 -----------4分
(Ⅱ)解: .
.
当 时,令
时,令 ,得到
,得到 ,
, .当
.当 变化时,
变化时, 的变化情况如下表:
的变化情况如下表:
所以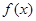 在区间
在区间 ,
, 内为减函数,在区间
内为减函数,在区间 内为增函数。8分
内为增函数。8分
函数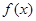 在
在 处取得极小值
处取得极小值 ,且
,且 ,
,
函数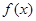 在
在 处取得极大值
处取得极大值 ,且
,且 . ------12分
. ------12分
(1)当
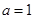 时,
时, ,
, ,
,又
 ,
, 从而点斜式得到结论。
从而点斜式得到结论。(2)当
 时,令
时,令 ,得到
,得到 ,
, 然后研究给定区间的单调性质得到极值。
然后研究给定区间的单调性质得到极值。(Ⅰ)解:当
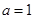 时,
时, ,
, ,
,又
 ,
, .
.所以,曲线
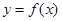 在点
在点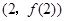 处的切线方程为
处的切线方程为 ,
,即
 。 -----------4分
。 -----------4分(Ⅱ)解:
 .
.当
 时,令
时,令 ,得到
,得到 ,
, .当
.当 变化时,
变化时, 的变化情况如下表:
的变化情况如下表: |  |  |  |  |  |
 |  | 0 |  | 0 |  |
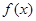 |  | 极小值 |  | 极大值 |  |
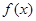 在区间
在区间 ,
, 内为减函数,在区间
内为减函数,在区间 内为增函数。8分
内为增函数。8分函数
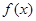 在
在 处取得极小值
处取得极小值 ,且
,且 ,
,函数
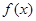 在
在 处取得极大值
处取得极大值 ,且
,且 . ------12分
. ------12分
练习册系列答案
 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案 欣语文化快乐暑假沈阳出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案
相关题目
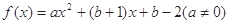 ,若存在实数
,若存在实数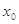 ,使
,使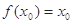 成立,则称
成立,则称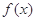 的不动点.
的不动点.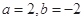 时,求
时,求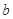 ,函数
,函数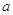 的取值范围;
的取值范围;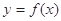 的图象上A、B两点的横坐标是函数
的图象上A、B两点的横坐标是函数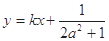 是线段AB的垂直平分线,求实数b的取值范围.
是线段AB的垂直平分线,求实数b的取值范围.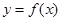 的周期为2,当
的周期为2,当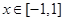 时
时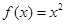 ,那么函数
,那么函数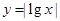 的图象的交点共有
的图象的交点共有 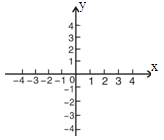
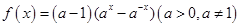 .
.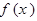 的奇偶性;
的奇偶性; 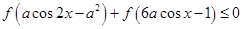 对任意
对任意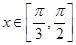 恒成立,求
恒成立,求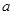 的取值范围.
的取值范围.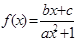 (
(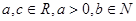 )是奇函数,
)是奇函数,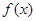 有最大值
有最大值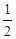
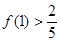 .
.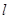 与
与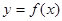 的图象交于P、Q两点,并且使得
的图象交于P、Q两点,并且使得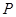 、
、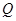 两点关于点
两点关于点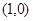 对称,若存在,求出直线
对称,若存在,求出直线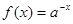
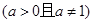 ,且
,且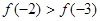 ,则
,则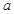 的取值范围是( )
的取值范围是( )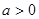
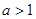
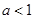
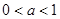
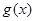 是定义在
是定义在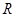 上、以2为周期的函数,若
上、以2为周期的函数,若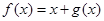 在
在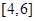 上的值域为
上的值域为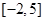 ,则
,则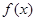 在区间
在区间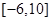 上的值域为 .
上的值域为 .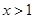 ,则函数
,则函数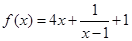 的最小值是( )
的最小值是( )