题目内容
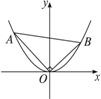
如图所示，求抛物线y2=2px（p＞0）和过它上面的点
的切线的垂线所围成的平面图形的面积．
【答案】分析：解出y，求出y′把P1坐标代入求出切线的斜率写出切线的方程，与抛物线方程y2=2px（p＞0）联立得到y的值，然后利用定积分求出面积即可．
解答：解：由题意令
，
，
，
所以过P1点且垂直于过P1点的抛物线的切线的直线的斜率为-1．
其方程为
．
即2x+2y-3p=0．
与抛物线方程联立消去x，得y2+2py-3p2=0，
解得y=p或y=-3p．
又
，
所以所求平面图形的面积为
=
=
=
．
点评：考查学生求直线方程的能力，以及抛物线的运用能力，利用定积分求图形面积的能力．
解答：解：由题意令
，，，所以过P1点且垂直于过P1点的抛物线的切线的直线的斜率为-1．
其方程为
．即2x+2y-3p=0．
与抛物线方程联立消去x，得y2+2py-3p2=0，
解得y=p或y=-3p．
又
，所以所求平面图形的面积为
==
=．点评：考查学生求直线方程的能力，以及抛物线的运用能力，利用定积分求图形面积的能力．
练习册系列答案
相关题目
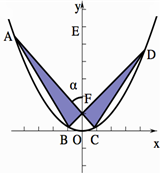某校同学设计一个如图所示的“蝴蝶形图案（阴影区域）”，其中AC、BD是过抛物线Γ焦点F的两条弦，且其焦点F（0，1），
