题目内容

在平面直角坐标系xOy中,抛物线y=x2上异于坐标原点O的两不同动点A、B满足AO⊥BO(如图所示).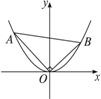

(1)求△AOB的重心G(即三角形三条中线的交点)的轨迹方程.

(2)△AOB的面积是否存在最小值?若存在,请求出最小值;若不存在,请说明理由.

解:(1)设△AOB的重心为G(x,y),A(x1,y1),B(x2,y2),则①

∵OA⊥OB,=(x1,y1),=(x2,y2),·=0,即x1x2+y1y2=0.②

又点A、B在抛物线上,有y1=x12,y2=x22,代入②化简,得x1x2=-1,

∴y==(x12+x22)=［(x1+x2)2-2x1x2］=×(3x)2+=3x2+.

∴重心为G的轨迹方程为y=3x2+.

(2)S△AOB=OA·OB==,

由(1)得S△AOB=≥

==×2=1.

当且仅当x12=x22,即x1=-x2=-1时,等号成立.

∴△AOB的面积存在最小值,存在时其最小值为1.

练习册系列答案
相关题目
在平面直角坐标系xoy中，已知圆心在直线y=x+4上，半径为2
2
的圆C经过坐标原点O，椭圆
x2
a2
+
y2
9
=1(a＞0)与圆C的一个交点到椭圆两焦点的距离之和为10．
（1）求圆C的方程；
（2）若F为椭圆的右焦点，点P在圆C上，且满足PF=4，求点P的坐标．
如图，在平面直角坐标系xOy中，锐角α和钝角β的终边分别与单位圆交于A，B两点．若点A的横坐标是
3
5
，点B的纵坐标是
12
13
，则sin（α+β）的值是
16
65
16
65
．
在平面直角坐标系xOy中，若焦点在x轴的椭圆
x2
m
+
y2
3
=1的离心率为
1
2
，则m的值为
4
4
．
（2013•泰州三模）选修4-4：坐标系与参数方程
在平面直角坐标系xOy中，已知A（0，1），B（0，-1），C（t，0），D(
3t
，0)，其中t≠0．设直线AC与BD的交点为P，求动点P的轨迹的参数方程（以t为参数）及普通方程．
（2013•东莞一模）在平面直角坐标系xOy中，已知椭圆C：
x2
a2
+
y2
b2
=1(a＞b＞0)的左焦点为F1（-1，0），且椭圆C的离心率e=
1
2
．
（1）求椭圆C的方程；
（2）设椭圆C的上下顶点分别为A1，A2，Q是椭圆C上异于A1，A2的任一点，直线QA1，QA2分别交x轴于点S，T，证明：|OS|•|OT|为定值，并求出该定值；
（3）在椭圆C上，是否存在点M（m，n），使得直线l：mx+ny=2与圆O：x2+y2=
16
7
相交于不同的两点A、B，且△OAB的面积最大？若存在，求出点M的坐标及对应的△OAB的面积；若不存在，请说明理由．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网