题目内容
(本小题满分14分)已知集合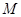 是满足下列性质的函数
是满足下列性质的函数 的全体:在定义域内存在
的全体:在定义域内存在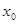 ,使得
,使得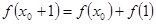 成立。
成立。
(Ⅰ)函数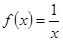 是否属于集合
是否属于集合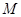 ?说明理由;
?说明理由;
(Ⅱ)设函数 ,求
,求 的取值范围;
的取值范围;
(Ⅲ)设函数 图象与函数
图象与函数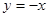 的图象有交点,
的图象有交点,
证明:函数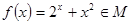 。
。
(Ⅰ)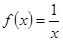
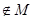 。(Ⅱ)
。(Ⅱ)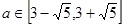 。 (Ⅲ)见解析。
。 (Ⅲ)见解析。
解析试题分析:(1)根据题意,只要sin(x0+1)=sinx0+sin1成立即可,由解析式列出方程,再由特殊角的正弦值进行证明;
(2)把解析式代入f(x+1)=f(x)+f(1),列出对应的方程,再由一元二次方程有解的条件求出k的范围,注意二次系数是否为零;
(3)根据定义只要证明f(x+1)=f(x)+f(1)有解,把解析式代入列出方程,转化为对应的函数,利用函数的零点存在性判定理进行判断..
(Ⅰ)若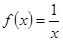
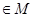 ,在定义域内存在
,在定义域内存在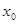 ,则
,则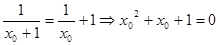 , ∵方程
, ∵方程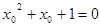 无解,∴
无解,∴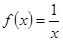
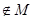 。
。
(Ⅱ)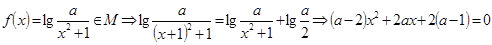 ,
,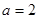 时,
时,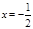 ;
;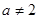 时,由
时,由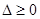 ,得
,得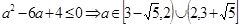 。
。
∴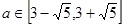 。
。
(Ⅲ)∵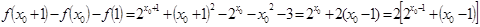 ,
,
又∵函数 图象与函数
图象与函数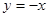 的图象有交点,设交点的横坐标为
的图象有交点,设交点的横坐标为 ,
,
则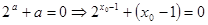 ,其中
,其中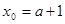 。
。
∴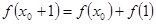 ,即
,即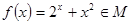 。
。
考点:对数函数图像与性质的综合应用.
点评:本题属于新定义,新情景的问题,主要利用新定义进行运算,考查了对数函数、正弦函数和指数函数的性质,函数的零点存在性判定理的应用,综合性强、难度大.

练习册系列答案
 长江作业本同步练习册系列答案
长江作业本同步练习册系列答案
相关题目
(本小题12分)
某市居民生活用水收费标准如下:
用水量 (吨) (吨) | 每吨收费标准(元) |
不超过 吨部分 吨部分 |  |
超过 吨不超过 吨不超过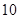 吨部分 吨部分 | 3 |
超过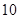 吨部分 吨部分 | 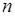 |
 吨,缴纳的水费为
吨,缴纳的水费为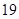 元;二月份用水量为
元;二月份用水量为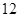 吨,缴纳的水费为
吨,缴纳的水费为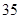 元.设某用户月用水量为
元.设某用户月用水量为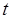 吨,交纳的水费为
吨,交纳的水费为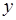 元.
元.(1)写出
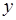 关于
关于 的函数关系式;
的函数关系式;(2)若某用户希望三月份缴纳的水费不超过
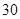 元,求该用户三月份最多可以用多少吨水?
元,求该用户三月份最多可以用多少吨水? 
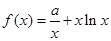 ,
,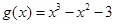 .
.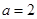 时,求曲线
时,求曲线 在
在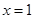 处的切线的斜率;
处的切线的斜率;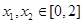 ,使得
,使得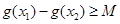 成立,求满足上述条件的最大整数
成立,求满足上述条件的最大整数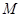 ;
;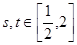 ,都有
,都有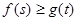 成立,求实数
成立,求实数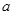 的取值范围.
的取值范围.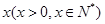 户农民从事蔬菜加工,则剩下的继续从事蔬菜种植的农民平均每户的年收入有望提高
户农民从事蔬菜加工,则剩下的继续从事蔬菜种植的农民平均每户的年收入有望提高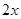 %,而从事蔬菜加工的农民平均每户的年收入将为
%,而从事蔬菜加工的农民平均每户的年收入将为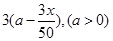 万元.
万元. 户农民从事蔬菜加工后,要使从事蔬菜种植的农民的总年收入不低于动员前从事蔬菜种植的农民的总年收入,求
户农民从事蔬菜加工后,要使从事蔬菜种植的农民的总年收入不低于动员前从事蔬菜种植的农民的总年收入,求 的最大值.
的最大值. 定义在
定义在 上,对于任意实数
上,对于任意实数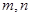 ,恒有
,恒有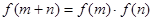 ,且当
,且当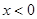 时,
时,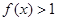
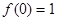 ,且当
,且当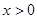 时,
时, 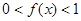
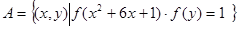 ,
,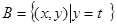 ,且
,且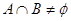 ,
, 的取值范围.
的取值范围. 元/本(9≤
元/本(9≤ 万本.
万本. (万元)与每本书的定价
(万元)与每本书的定价 的图象经过点
的图象经过点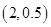 ,其中
,其中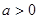 且
且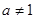 。
。 的值;
的值; 百件时,若
百件时,若 ,则销售所得的收入为
,则销售所得的收入为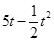 万元:若
万元:若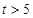 ,则销售收入为
,则销售收入为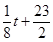 万元.
万元.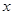 百件
百件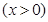 ,请把该公司生产并销售这种产品所得的年利润
,请把该公司生产并销售这种产品所得的年利润 表示为当年生产量
表示为当年生产量