题目内容
(本小题满分15分)设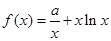 ,
,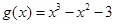 .
.
(1)当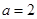 时,求曲线
时,求曲线 在
在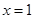 处的切线的斜率;
处的切线的斜率;
(2)如果存在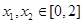 ,使得
,使得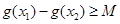 成立,求满足上述条件的最大整数
成立,求满足上述条件的最大整数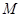 ;
;
(3)如果对于任意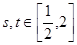 ,都有
,都有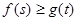 成立,求实数
成立,求实数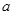 的取值范围.
的取值范围.
(1)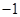 (2)
(2) (3)
(3)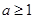
解析试题分析:(1)当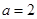 时,
时,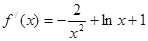 ,故
,故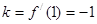 . ……3分
. ……3分
(2)存在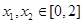 ,使得
,使得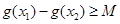 成立等价于
成立等价于 ,
,
∵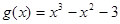 ,∴
,∴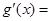
 ,
,
∴ 在
在 上单调递减,在
上单调递减,在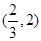 上单调递增, ……6分
上单调递增, ……6分
∴ ,
,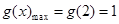 ,
,
∴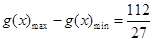 ,
,
∴满足的最大整数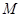 为4; ……8分
为4; ……8分
(3)对于任意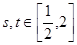 ,都有
,都有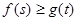 成立,等价于
成立,等价于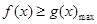 .
.
由(2)知,在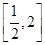 上,
上,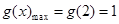 ,
,
∴在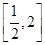 上,
上,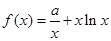
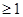 恒成立,等价于
恒成立,等价于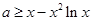 恒成立,
恒成立,
记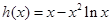 ,则
,则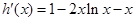 且
且 ,
,
∴当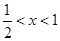 时,
时, ;当
;当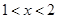 时,
时, ,
,
∴函数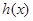 在
在 上单调递增,在
上单调递增,在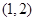 上单调递减,
上单调递减,
∴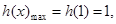 ∴
∴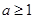 . ……15分
. ……15分
考点:本小题主要考查导数的几何意义的应用和利用导数解决单调性、最值和恒成立等问题,考查学生综
合运算所学知识分析问题、解决问题的能力和运算求解能力.
点评:恒成立问题是高考中一个常考的考点,恒成立问题一般转化成最值问题来解决.导数是研究函数性
质尤其是单调性、最值问题的有力工具,要灵活运算,但是不要忘记定义域.

练习册系列答案
相关题目
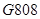 次列车在平直的铁轨上匀速行驶,由于遇到紧急情况,紧急刹车时列车行驶的路程
次列车在平直的铁轨上匀速行驶,由于遇到紧急情况,紧急刹车时列车行驶的路程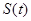 (单位:
(单位: )和时间
)和时间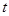 (单位:
(单位: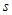 )的关系为:
)的关系为: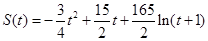 .
.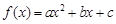 , 满足
, 满足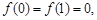 且
且 的最小值是
的最小值是 .(Ⅰ)求
.(Ⅰ)求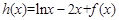 ,若函数
,若函数 在区间
在区间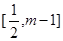 上是单调函数,求实数
上是单调函数,求实数 的取值范围。
的取值范围。 ax2+3x+5(a>0).
ax2+3x+5(a>0).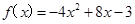 .
.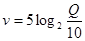 ,单位是
,单位是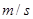 ,其中
,其中 表示燕子的耗氧量。
表示燕子的耗氧量。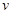 (单位:千米/小时)是车流密度
(单位:千米/小时)是车流密度 (单位:辆/千米)的函数.当桥上的车流密度达到200辆/千米时,造成堵塞,此时车流速度为0;当车流密度不超过20辆/千米时,车流速度为60千米/小时.研究表明:当
(单位:辆/千米)的函数.当桥上的车流密度达到200辆/千米时,造成堵塞,此时车流速度为0;当车流密度不超过20辆/千米时,车流速度为60千米/小时.研究表明:当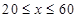 时,车流速度
时,车流速度 的表达式;
的表达式;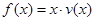 可以达到最大,并求出最大值.(精确到1辆/小时)
可以达到最大,并求出最大值.(精确到1辆/小时)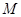 是满足下列性质的函数
是满足下列性质的函数 的全体:在定义域内存在
的全体:在定义域内存在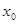 ,使得
,使得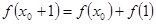 成立。
成立。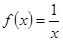 是否属于集合
是否属于集合 ,求
,求 的取值范围;
的取值范围; 图象与函数
图象与函数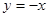 的图象有交点,
的图象有交点,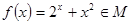 。
。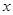 (百台),其总成本为
(百台),其总成本为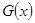 (万元),其中固定成本为2.8万元,并且每生产1百台的生产成本为2万元(总成本=固定成本+生产成本).销售收入
(万元),其中固定成本为2.8万元,并且每生产1百台的生产成本为2万元(总成本=固定成本+生产成本).销售收入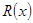 (万元)满足
(万元)满足 ,假定该产品产销平衡(即生产的产品都能卖掉),根据上述统计规律,请完成下列问题:
,假定该产品产销平衡(即生产的产品都能卖掉),根据上述统计规律,请完成下列问题: 的解析式(利润=销售收入—总成本);
的解析式(利润=销售收入—总成本);