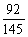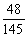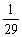题目内容
某学校的三个学生社团的人数分布如下表(每名学生只能参加一个社团):
| 围棋社 | 舞蹈社 | 拳击社 |
男生 | 5 | 10 | 28 |
女生 | 15 | 30 | m |
学校要对这三个社团的活动效果进行抽样调查,按分层抽样的方法从三个社团成员中抽取18人,结果拳击社被抽出了6人.
(Ⅰ)求拳击社团被抽出的6人中有5人是男生的概率;
(Ⅱ)设拳击社团有X名女生被抽出,求X的分布列及数学期望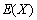 .
.
【答案】
(Ⅰ)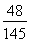 ;(Ⅱ)
;(Ⅱ)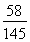 .
.
【解析】
试题分析:(Ⅰ)先根据分层抽样的特点求出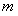 的值,然后利用古典概型及其概率计算公式进行求解即可;
的值,然后利用古典概型及其概率计算公式进行求解即可;
(Ⅱ)由题意可知: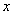 =0,1,2,然后根据古典概型及其概率计算公式分别求出相应的概率,写出分布列,最后利用数学期望公式解之即可.
=0,1,2,然后根据古典概型及其概率计算公式分别求出相应的概率,写出分布列,最后利用数学期望公式解之即可.
试题解析:解:(Ⅰ)由于按分层抽样的方法从三个社团成员中抽取18人,拳击社被抽出了6人

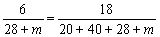

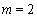 3分
3分
设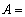 “拳击社团被抽出的6人中有5人是男生”
“拳击社团被抽出的6人中有5人是男生”
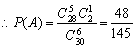 6分
6分
(Ⅱ)由题意可知: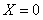 ,1,2
,1,2
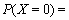
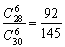 ,
, 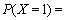
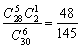
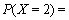
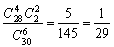 9分
9分
X | 0 | 1 | 2 |
P |
|
|
|
-11分
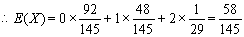 12分
12分
考点:1、离散型随机变量及其分布列;2、古典概型及其概率计算公式;3、离散型随机变量的期望与方差.

练习册系列答案
相关题目
某学校三个社团的人员分布如下表(每名同学只参加一个社团)
学校要对这三个社团的活动效果进行抽样调查,按分层抽样的方法从社团成员中抽取30人,结果围棋社被抽出12人.
(I) 求这三个社团共有多少人?
(II) 书法社从3名高中和2名初中成员中,随机选出2人参加书法展示,求这2人中初、高中学生都有的概率.
| 围棋社 | 戏剧社 | 书法社 | |
| 高中 | 45 | 30 | a |
| 初中 | 15 | 10 | 20 |
(I) 求这三个社团共有多少人?
(II) 书法社从3名高中和2名初中成员中,随机选出2人参加书法展示,求这2人中初、高中学生都有的概率.
某学校的三个学生社团的人数分布如下表(每名学生只能参加一个社团):
| 围棋社 | 舞蹈社 | 拳击社 |
男生 | 5 | 10 | 28 |
女生 | 15 | 30 | m |
学校要对这三个社团的活动效果进行抽样调查,按分层抽样的方法从三个社团成员中抽取18人,结果拳击社被抽出了6人.
(Ⅰ)求拳击社女生有多少人;
(Ⅱ)从围棋社指定的3名男生和2名女生中随机选出2人参加围棋比赛,求这两名同学是一名男生和一名女生的概率.