题目内容
某班共有学生40人,将以此数学考试成绩(单位:分)绘制成频率分布直方图,如图所示.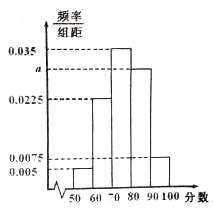
(1)请根据图中所给的数据,求a的值;
(2)从成绩在[50,70)内的学生中随机选3名学生,求这3名学生的成绩都在[60,70)内的概率;
(3)为了了解学生这次考试的失分情况,从成绩在[50,70)内的学生中随机选取3人的成绩进行分析,用X表示所选学生成绩在[60,70)内的人数,求X的分布列和数学期望.
(1)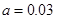 (2)
(2)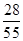 (3)
(3)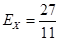
解析试题分析:
(1)频率分布直方图的纵坐标为频率与组距之比,故可以求的每组的频率,根据每个组的概率之和为1可以求的a的值.
(2)从频率分布直方图中可以得到[50,70)被分为两组[50,60)与[60,70)和两组的频率,频率乘以总数40人就可以得到各组的人数,在两组中无序的抽3人可以用组合数算得总的基本事件数,再用组合数可以求的在[60,70)内抽取3人的基本事件数,再利用古典概型的概率计算公式,即可得到该事件的概率.
(3)由第二问可知X的可能取值为1,2,3,再采用与第二问相同的方法可以算的X取1,2,3时,的概率得到分布列,进而得到期望.
试题解析:
(1)根据频率分布直方图中的数据,可得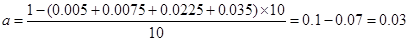 ,
,
所以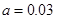 . 2分
. 2分
(2)学生成绩在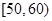 内的共有40×0.05=2人,在
内的共有40×0.05=2人,在 内的共有40×0.225=9人,
内的共有40×0.225=9人,
成绩在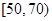 内的学生共有11人. 4分
内的学生共有11人. 4分
设“从成绩在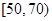 的学生中随机选3名,且他们的成绩都在
的学生中随机选3名,且他们的成绩都在 内”为事件A,
内”为事件A,
则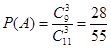 .
.
所以选取的3名学生成绩都在 内的概率为
内的概率为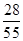 . 6分
. 6分
(3)依题意,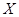 的可能取值是1,2,3. 7分
的可能取值是1,2,3. 7分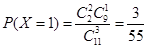 ;
;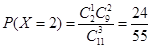 ;
;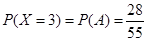 . 10分
. 10分
所以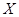 的分布列为
的分布列为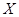
1 2 3 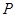
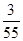
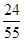
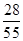
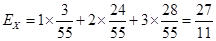 . 12分
. 12分
考点:古典概型分布列期望频率分布直方图

某校高三年级一次数学考试后,为了解学生的数学学习情况,随机抽取 名学生的数学成绩,制成表所示的频率分布表.
名学生的数学成绩,制成表所示的频率分布表.
| 组号 | 分组 | 频数 | 频率 |
| 第一组 |  |  |  |
| 第二组 |  |  |  |
| 第三组 |  |  |  |
| 第四组 |  | 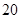 |  |
| 第五组 |  |  |  |
| 合计 |  |  | |
 、
、 、
、 的值;
的值;(2)若从第三、四、五组中用分层抽样方法抽取
 名学生,并在这
名学生,并在这 名学生中随机抽取
名学生中随机抽取 名学生与张老师面谈,求第三组中至少有
名学生与张老师面谈,求第三组中至少有 名学生与张老师面谈的概率
名学生与张老师面谈的概率 想象一下一个人从出生到死亡,在每个生日都测量身高,并作出这些数据的散点图,这些点将不会落在一条直线上,但在一段时间内的增长数据有时可以用线性回归来分析,下表是一位母亲给儿子做的成长记录:
| 年龄/周岁 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 身高/cm | 91.8 | 97.6 | 104.2 | 110.9 | 115.6 | 122.0 | 128.5 |
| | |||||||
| 年龄/周岁 | 10 | 11 | 12 | 13 | 14 | 15 | 16 |
| 身高/cm | 134.2 | 140.8 | 147.6 | 154.2 | 160.9 | 167.5 | 173.0 |
(2)如果年龄相差5岁,则身高有多大差异(3~16岁之间)?
(3)如果身高相差20 cm,其年龄相差多少(3~16岁之间)?
(4)计算残差,说明该函数模型是否能够较好地反映年龄与身高的关系,说明理由.
对196个接受心脏搭桥手术的病人和196个接受血管清障手术的病人进行了3年的跟踪研究,调查他们是否又发作过心脏病,调查结果如下所示:
| | 又发作过心脏病 | 未发作过心脏病 | 合计 |
| 心脏搭桥手术 | 39 | 157 | 196 |
| 血管清障手术 | 29 | 167 | 196 |
| 合计 | 68 | 324 | 392 |
从一批苹果中,随机抽取50个,其重量(单位:克)的频数分布表如下:
| 分组(重量) |  |  |  |  |
| 频数(个) | 5 | 10 | 20 | 15 |
 的频率;
的频率;(2)用分层抽样的方法从重量在
 和
和 的苹果中共抽取4个,其中重量在
的苹果中共抽取4个,其中重量在 的有几个?
的有几个?(3)在(2)中抽出的4个苹果中,任取2个,求重量在
 和
和 中各有1个的概率.
中各有1个的概率. 研究性学习小组为了解某生活小区居民用水量 (吨)与气温
(吨)与气温 (℃)之间的关系,随机统计并制作了5天该小区居民用水量与当天气温的对应表:
(℃)之间的关系,随机统计并制作了5天该小区居民用水量与当天气温的对应表:
| 日期 | 9月5日 | 10月3日 | 10月8日 | 11月16日 | 12月21日 |
气温 (℃) (℃) | 18 | 15 | 11 | 9 | -3 |
用水量 (吨) (吨) | 57 | 46 | 36 | 37 | 24 |
(2)由表中数据求得线性回归方程
 中的
中的 ,试求出
,试求出 的值,并预测当地气温为5℃时,该生活小区的用水量.
的值,并预测当地气温为5℃时,该生活小区的用水量.  份试卷进行成绩分析,得到数学成绩频率分布直方图(如图所示),其中成绩在
份试卷进行成绩分析,得到数学成绩频率分布直方图(如图所示),其中成绩在 的学生人数为6.
的学生人数为6. 和
和 这两组中共抽取5个学生,并从这5个学生中任取2人进行点评,求分数在
这两组中共抽取5个学生,并从这5个学生中任取2人进行点评,求分数在
 表示.
表示.
 ,求
,求
 ;
;