题目内容
如图所示的茎叶图记录了甲、乙两组各四名同学的投篮命中次数,乙组记录中有一个数据模糊,无法确认,在图中以 表示.
表示.
(1)如果乙组同学投篮命中次数的平均数为 ,求
,求 及乙组同学投篮命中次数的方差;
及乙组同学投篮命中次数的方差;
(2)在(1)的条件下,分别从甲、乙两组投篮命中次数低于10次的同学中,各随机选取一名,求这两名同学的投篮命中次数之和为17的概率.
(1) ,方差
,方差 .(2)
.(2) .
.
解析试题分析:(1)由 ,得
,得 ,
,
应用方差计算公式可得 .
.
(2)记甲组投篮命中次数低于10次的同学为 ,他们的命中次数分别为9,7.
,他们的命中次数分别为9,7.
乙组投篮命中次数低于10次的同学为 ,他们的命中次数分别为8,8,9.
,他们的命中次数分别为8,8,9.
依题意,不同的选取方法有: ,
, 共6种. 9分
共6种. 9分
设“这两名同学的投篮命中次数之和为17”为事件C,则C中恰含有 共2种.
共2种.
由古典概型概率的计算公式可得.
试题解析:(1)依题意得: ,解得
,解得 , 3分
, 3分
方差 . 6分
. 6分
(2)记甲组投篮命中次数低于10次的同学为 ,他们的命中次数分别为9,7.
,他们的命中次数分别为9,7.
乙组投篮命中次数低于10次的同学为 ,他们的命中次数分别为8,8,9.
,他们的命中次数分别为8,8,9.
依题意,不同的选取方法有: ,
, 共6种. 9分
共6种. 9分
设“这两名同学的投篮命中次数之和为17”为事件C,则C中恰含有 共2种.
共2种. . 12分
. 12分
考点:茎叶图,方差,古典概型概率的计算.

 名校名师培优作业本加核心试卷系列答案
名校名师培优作业本加核心试卷系列答案 全程金卷系列答案
全程金卷系列答案我校为了了解高二级学生参加体育活动的情况,随机抽取了100名高二级学生进行调查.下面是根据调查结果绘制的学生日均参加体育活动时间的频率分布直方图: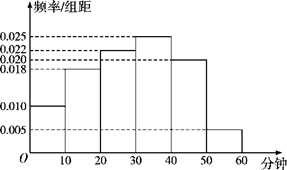
将日均参加体育活动时间不低于40分钟的学生称为参加体育活动的“积极分子”.根据已知条件完成下面的列联表,并据此资料,在犯错误的概率不超过5%的前提下,你是否认为参加体育活动的“积极分子”与性别有关?
| | 非积极分子 | 积极分子 | 合计 |
| 男 | | 15 | 45 |
| 女 | | | |
| 合计 | | | |
户外运动已经成为一种时尚运动,某单位为了了解员工喜欢户外运动是否与性别有关,决定从本单位全体650人中采用分层抽样的办法抽取50人进行问卷调查,得到了如下列联表:
| | 喜欢户外运动 | 不喜欢户外运动 | 合计 |
| 男性 | | 5 | |
| 女性 | 10 | | |
| 合计 | | | 50 |
 .
.(1)请将上面的列联表补充完整;(2)求该公司男、女员工各多少名;
(3)是否有
 的把握认为喜欢户外运动与性别有关?并说明你的理由.
的把握认为喜欢户外运动与性别有关?并说明你的理由.下面的临界值表仅供参考:
 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
 ,其中
,其中 .
. 城市公交车的数量若太多则容易造成资源的浪费;若太少又难以满足乘客需求.某市公交公司在某站台的60名候车乘客中随机抽取15人,将他们的候车时间作为样本分成5组,如下表所示(单位:分钟):
| 组别 | 候车时间 | 人数 |
| 一 |  | 2 |
| 二 |  | 6 |
| 三 |  | 4 |
| 四 |  | 2 |
| 五 |  | 1 |
(2)若从上表第三、四组的6人中任选2人作进一步的调查,求抽到的两人恰好来自不同组的概率.
某中学举行了一次“环保知识竞赛”, 全校学生参加了这次竞赛.为了了解本次竞赛成绩情况,从中抽取了部分学生的成绩(得分取正整数,满分为100分)作为样本进行统计.请根据下面尚未完成并有局部污损的频率分布表和频率分布直方图(如图所示)解决下列问题:
| 组别 | 分组 | 频数 | 频率 |
| 第1组 | [50,60) | 8 | 0 16 |
| 第2组 | [60,70) | a | ▓ |
| 第3组 | [70,80) | 20 | 0 40 |
| 第4组 | [80,90) | ▓ | 0 08 |
| 第5组 | [90,100] | 2 | b |
| | 合计 | ▓ | ▓ |

(1)求出
 的值;
的值;(2)在选取的样本中,从竞赛成绩是80分以上(含80分)的同学中随机抽取2名同学到广场参加环保知识的志愿宣传活动
(ⅰ)求所抽取的2名同学中至少有1名同学来自第5组的概率;
(ⅱ)求所抽取的2名同学来自同一组的概率

 为这两位同学中成绩低于平均分的人数,求
为这两位同学中成绩低于平均分的人数,求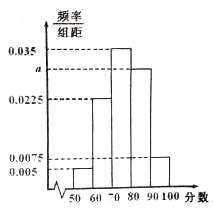
 技术规定》 (试行),
技术规定》 (试行), 为优,
为优, 为良,
为良, 为轻度污染,
为轻度污染, 为中度污染,
为中度污染, ,
, 均为重度污染,
均为重度污染, 及以上为严重污染.某市2013年11月份
及以上为严重污染.某市2013年11月份 天的
天的
 天进行市民户外晨练人数调查,则中度污染被抽到的天数共有多少天?
天进行市民户外晨练人数调查,则中度污染被抽到的天数共有多少天? 时市民适宜户外晨练,若市民王先生决定某天早晨进行户外晨练,则他当天适宜户外晨练的概率是多少?
时市民适宜户外晨练,若市民王先生决定某天早晨进行户外晨练,则他当天适宜户外晨练的概率是多少?
 ,求恰有一名同学获得该高校B类资格的概率.
,求恰有一名同学获得该高校B类资格的概率.