题目内容

设
OA
=
a
，
OB
=
b
，
OC
=
c
，当
c
=λ
a
+μ
b
，且λ+μ=1时，点C在（　　）
分析：利用向量的运算法则得到
AC
=u
AB
，利用向量共线的充要条件判断出两个向量共线，得到三点共线．
解答：解：∵λ+μ=1∴λ=1-μ，∴
c
=(1-μ)
a
+μ
b

即
c
-
a
=μ(
b
-
a
)，所以
OC
-
OA
═μ(
OB
-
OA
)，
AC
=u
AB
，
∴A，B，C共线
故选A
点评：本题考查向量的运算法则、向量共线的充要条件、利用向量共线判断三点共线
练习册系列答案
相关题目
平面上有一个△ABC和一点O，设
OA
=
a
，
OB
=
b
，
OC
=
c
，又OA、BC的中点分别为D、E，则向量
DE
等于（　　）
A、
1
2
(
a
+
b
+
c
)
B、
1
2
(-
a
+
b
+
c
)
C、
1
2
(
a
-
b
+
c
)
D、
1
2
(
a
+
b
+
c
)
已知三棱锥O-ABC，点G是△ABC的重心．设
OA
=a，
OB
=b，
OC
=c，那么向量
OG
用基底{a，b，c}可以表示为（　　）精英家教网
A、
1
2
a+
1
2
b+
1
3
c
B、
1
3
a+
1
3
b+
1
3
c
C、
1
2
a+
1
2
b+
1
2
c
D、
2
3
a+
2
3
b+
2
3
c
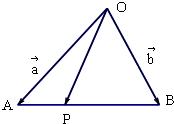在△OAB中，点P在边AB上，
PB
=3
AP
，设
OA
=a，
OB
=b，则
OP
=（　　）
已知O，A，B三点不共线，且满足：
OC
=2
OA
，
OD
=3
OB
，设
OA
=
a
，
OB
=
b
，若直线AD与BC相交于点E，则向量
OE
=
4
5
a
+
3
5
b
4
5
a
+
3
5
b
．（用向量
a
，
b
表示）

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网