题目内容
平面上有一个△ABC和一点O,设
=
,
=
,
=
,又OA、BC的中点分别为D、E,则向量
等于( )
| OA |
| a |
| OB |
| b |
| OC |
| c |
| DE |
A、
| ||||||||
B、
| ||||||||
C、
| ||||||||
D、
|
分析:利用E为BC的中点,D为OA的中点,
=
(
+
),
=-
,化简可得结果.
| OE |
| 1 |
| 2 |
| OB |
| OC |
| DO |
| 1 |
| 2 |
| OA |
解答:解:∵
=a,
=b,
=c,E为BC的中点,D为OA的中点,
∴
=
(
+
),
=-
,
∴
=
+
=
(-
+
+
)
故选B.
| OA |
| OB |
| OC |
∴
| OE |
| 1 |
| 2 |
| OB |
| OC |
| DO |
| 1 |
| 2 |
| OA |
∴
| DE |
| DO |
| OE |
| 1 |
| 2 |
| a |
| b |
| c |
故选B.
点评:本题考查向量中点公式的应用,以及两个向量的加减法的法则和几何意义.

练习册系列答案
相关题目
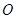 ,设
,设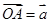 ,
,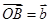 ,
,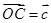 ,又
,又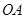 、
、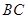 的中点分别为
的中点分别为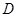 、
、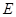 ,则向量
,则向量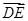 等于( )
等于( )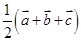 B.
B.
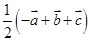
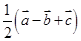 D.
D. 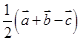
 ,又OA、BC的中点分别为D、E,则向量
,又OA、BC的中点分别为D、E,则向量 等于( )
等于( )



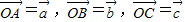 ,又OA、BC的中点分别为D、E,则向量
,又OA、BC的中点分别为D、E,则向量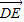 等于( )
等于( )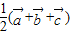
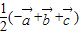
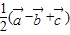
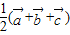
 ,又OA、BC的中点分别为D、E,则向量
,又OA、BC的中点分别为D、E,则向量 等于( )
等于( )


