题目内容
已知O，A，B三点不共线，且满足：
=2
，
=3
，设
=
，
=
，若直线AD与BC相交于点E，则向量
=
+
+
．（用向量
，
表示）
| OC |
| OA |
| OD |
| OB |
| OA |
| a |
| OB |
| b |
| OE |
| 4 |
| 5 |
| a |
| 3 |
| 5 |
| b |
| 4 |
| 5 |
| a |
| 3 |
| 5 |
| b |
| a |
| b |
分析：设
=λ
，利用向量的减法法则并结合题意，算出
=
+
．再设
=μ
，同样的方法算出
=
+
，根据平面向量基本定理解出λ、μ之值，即可得到
用
、
表达的式子．
| BE |
| EC |
| OE |
| 1 |
| 1+λ |
| b |
| 2λ |
| 1+λ |
| a |
| AE |
| ED |
| OE |
| 3μ |
| 1+μ |
| b |
| 1 |
| 1+μ |
| a |
| OE |
| a |
| b |
解答：解：设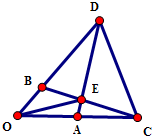
=λ
，则
-
=λ(
-
)
化简得
=
+
=
+
∵
=
，
=
，
∴
=
+
再设
=μ
，同理算出
=
+
根据平面向量基本定理，得
=
且
=
解之得λ=
，μ=
．由此可得
=
+
故答案为：
+
| BE |
| EC |
| OE |
| OB |
| OC |
| OE |
化简得
| OE |
| 1 |
| 1+λ |
| OB |
| λ |
| 1+λ |
| OC |
| 1 |
| 1+λ |
| OB |
| 2λ |
| 1+λ |
| OA |
∵
| OA |
| a |
| OB |
| b |
∴
| OE |
| 1 |
| 1+λ |
| b |
| 2λ |
| 1+λ |
| a |
再设
| AE |
| ED |
| OE |
| 3μ |
| 1+μ |
| b |
| 1 |
| 1+μ |
| a |
根据平面向量基本定理，得
| 1 |
| 1+λ |
| 3μ |
| 1+μ |
| 2λ |
| 1+λ |
| μ |
| 1+μ |
解之得λ=
| 2 |
| 3 |
| 1 |
| 4 |
| OE |
| 4 |
| 5 |
| a |
| 3 |
| 5 |
| b |
故答案为：
| 4 |
| 5 |
| a |
| 3 |
| 5 |
| b |
点评：本题给出三角形边的中点和三等分点，求用
、
表示
的式子．着重考查了平面向量的减法法则和平面向量的基本定理及其意义等知识点，属于基础题．
| a |
| b |
| OE |
练习册系列答案
名校课堂系列答案
相关题目
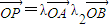则λ1+λ2=1，类比该定理进行研究，可以得出：已知O、A、B三点不共线，若点P、O在直线AB同侧（点P不在直线AB上），且
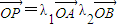，则 ．