题目内容
14.已知点A(2,1)为椭圆G:x2+2y2=m上的一点.(Ⅰ)求椭圆G的焦点坐标;
(Ⅱ)若椭圆G上的B,C两点满足2k1k2=-1(其中k1,k2分别为直线AB,AC的斜率).证明:B,C,O三点共线.
分析 (Ⅰ)由点A(2,1)为椭圆G:x2+2y2=m上的一点,求出m,由此能求出椭圆G的焦点坐标.
(Ⅱ)由$\left\{\begin{array}{l}{y={k}_{1}(x-2)+1}\\{{x}^{2}+{2y}^{2}=6}\end{array}\right.$,得$(2{{k}_{1}}^{2}+1){x}^{2}-4{k}_{1}(2{k}_{1}-1)x+2(2{k}_{1}-1)$2-6=0,由此利用韦达定理能推导出y1=-y2,从而能证明B、C、O三点共线.
解答 解:(Ⅰ)∵点A(2,1)为椭圆G:x2+2y2=m上的一点,
∴m=4+2=6,
∴椭圆的标准方程为$\frac{{x}^{2}}{6}+\frac{{y}^{2}}{3}=1$,
∴c=$\sqrt{6-3}=\sqrt{3}$,
∴椭圆G的焦点坐标为(-$\sqrt{3}$,0)和($\sqrt{3}$,0).
(Ⅱ)设B(x1,y1),C(x2,y2),
由$\left\{\begin{array}{l}{y={k}_{1}(x-2)+1}\\{{x}^{2}+{2y}^{2}=6}\end{array}\right.$,消去y,化简,得:
$(2{{k}_{1}}^{2}+1){x}^{2}-4{k}_{1}(2{k}_{1}-1)x+2(2{k}_{1}-1)$2-6=0,
∴${x}_{1}=\frac{(2{k}_{1}-1)^{2}-3}{2{{k}_{2}}^{2}+1}$,同理得${x}_{2}=\frac{(2{k}_{2}-1)^{2}-3}{2{{k}_{2}}^{2}+1}$,
∵2k1k2=-1,
∴${x}_{2}=\frac{2{{k}_{1}}^{2}(2{k}_{2}-1)^{2}-6{{k}_{1}}^{2}}{4{{k}_{1}}^{2}{{k}_{2}}^{2}+2{{k}_{1}}^{2}}$=$\frac{2(-1-{k}_{1})^{2}-6{{k}_{1}}^{2}}{1+2{{k}_{1}}^{2}}$=$\frac{2+4{k}_{1}-4{{k}_{1}}^{2}}{1+2{{k}_{1}}^{2}}$=$\frac{3-(2{k}_{1}-1)^{2}}{1+2{{k}_{1}}^{2}}$=-x1,
∴2k1k2=$2×\frac{{y}_{1}-1}{{x}_{1}-2}×\frac{{y}_{2}-1}{{x}_{2}-2}$=2×$\frac{({y}_{1}-1)({y}_{2}-1)}{4-{{x}_{1}}^{2}}$=$\frac{({y}_{1}-1)({y}_{2}-1)}{{{y}_{1}}^{2}-1}$=$\frac{{y}_{2}-1}{{y}_{1}+1}$=-1,
∴y1=-y2,
∴B、C、O三点共线.
点评 本题考查椭圆的焦点坐标的求法,考查三点共线的证明,是中档题,解题时要认真审题,注意椭圆性质的合理运用.

| A. | 8<$\frac{f(2)}{f(1)}$<16 | B. | 4<$\frac{f(2)}{f(1)}$<8 | C. | 3<$\frac{f(2)}{f(1)}$<4 | D. | 2<$\frac{f(2)}{f(1)}$<3 |
| A. | 关于点($\frac{π}{6}$,0)对称 | B. | 关于点($\frac{π}{3}$,0)对称 | ||
| C. | 关于直线x=$\frac{π}{6}$对称 | D. | 关于直线x=$\frac{π}{3}$对称 |
 如图,已知⊙C1:(x+$\sqrt{6}$)2+y2=32及点C2($\sqrt{6}$,0),在⊙C1上任取一点P,连结C2P,作线段C2P的中垂线交直线C1P于点M.
如图,已知⊙C1:(x+$\sqrt{6}$)2+y2=32及点C2($\sqrt{6}$,0),在⊙C1上任取一点P,连结C2P,作线段C2P的中垂线交直线C1P于点M. 已知椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)的长轴长为4,离心率为$\frac{1}{2}$.
已知椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)的长轴长为4,离心率为$\frac{1}{2}$.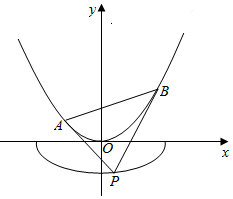 如图,已知曲线C1:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0,y≤0)的离心率e=$\frac{\sqrt{6}}{3}$,且经过点G(1,-$\frac{\sqrt{6}}{3}$),曲线C2:x2=2y,过曲线C1上一点P作C2的两条切线,切点分别为A,B.
如图,已知曲线C1:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0,y≤0)的离心率e=$\frac{\sqrt{6}}{3}$,且经过点G(1,-$\frac{\sqrt{6}}{3}$),曲线C2:x2=2y,过曲线C1上一点P作C2的两条切线,切点分别为A,B.