题目内容
设椭圆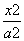 +
+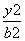 =1 (a>b>0)的左、右焦点分别是F1、F2,线段F1F2被点
=1 (a>b>0)的左、右焦点分别是F1、F2,线段F1F2被点 分成3∶1
分成3∶1
.2x-y-15=0
解析 设弦的两个端点分别为A(x1,y1),B(x2,y2),则x -4y
-4y =4,x
=4,x -4
-4 y
y =4,
=4,
两式相减得(x1+x2)(x1-x2)-4(y1+y2)(y1-y2)=0.
因为线段AB的中点为P(8,1),
所以x1+x2=16,y1+y2=2.
所 以
以 =2.
=2.
所以直线AB的方程为y-1=2(x-8),
代入x2-4y2=4满足Δ>0.
即2x-y-15=0.

练习册系列答案
相关题目
 >
> ,则a>b ③若a3>b3且ab<0,则
,则a>b ③若a3>b3且ab<0,则 >
> ④若a2>b2且ab>0,则
④若a2>b2且ab>0,则
 线y2=2px (p>0),O为抛物线的顶点,OA⊥OB,则直角三角形ABO的面积是________.
线y2=2px (p>0),O为抛物线的顶点,OA⊥OB,则直角三角形ABO的面积是________.
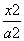 -
-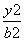 =1 (a>b>0)的离心率为
=1 (a>b>0)的离心率为 ,椭圆
,椭圆 ,求双曲线的标准方程.
,求双曲线的标准方程. 满足
满足 ,则
,则 的最大值是 .
的最大值是 .