题目内容
(本小题满分13分)
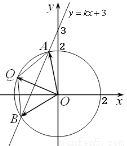
在平面直角坐标系 中,
中, 为坐标原点,以
为坐标原点,以 为圆心的圆与直线
为圆心的圆与直线 相切.
相切.
(Ⅰ)求圆 的方程;
的方程;
(Ⅱ)若直线 :
: 与圆
与圆 交于
交于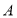 ,
, 两点,在圆
两点,在圆 上是否存在一点
上是否存在一点 ,使得
,使得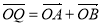 ,若存在,求出此时直线
,若存在,求出此时直线 的斜率;若不存在,说明理由.
的斜率;若不存在,说明理由.
(Ⅰ)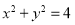 ;(Ⅱ)存在点
;(Ⅱ)存在点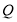 ,使得
,使得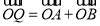 .
.
【解析】
试题分析:(Ⅰ)设圆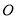 的半径为
的半径为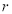 ,因为直线
,因为直线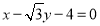 与圆
与圆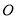 相切,所以
相切,所以 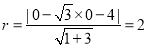 ,
,
即可求出圆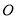 的方程为
的方程为 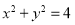 .(Ⅱ)方法一:因为直线
.(Ⅱ)方法一:因为直线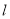 :
: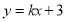 与圆
与圆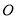 相交于
相交于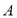 ,
,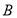 两点, 所以
两点, 所以 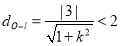 , 所以
, 所以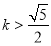 或
或 ,假设存在点
,假设存在点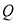 ,使得
,使得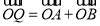 ,因为
,因为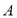 ,
,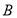 在圆上,且
在圆上,且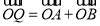 ,同时
,同时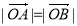 由向量加法的平行四边形法则可知,四边形
由向量加法的平行四边形法则可知,四边形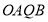 为菱形,所以
为菱形,所以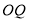 与
与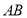 互相垂直且平分,所以原点
互相垂直且平分,所以原点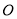 到直线
到直线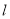 :
: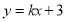 的距离为
的距离为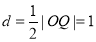 10分
10分
即 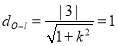 ,解得
,解得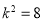 ,
, 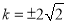 ,经验证满足条件,所以存在点
,经验证满足条件,所以存在点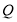 ,使得
,使得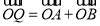 ;
;
方法二:假设存在点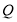 ,使得
,使得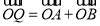 .记
.记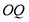 与
与 交于点
交于点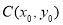 ,因为
,因为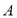 ,
,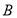 在圆上,且
在圆上,且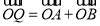 ,由向量加法的平行四边形法则可知四边形
,由向量加法的平行四边形法则可知四边形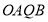 为菱形,因为直线
为菱形,因为直线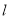 斜率为
斜率为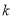 ,显然
,显然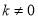 ,所以
,所以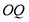 直线方程为
直线方程为 ,
, , 解得
, 解得 , 所以点
, 所以点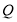 坐标为
坐标为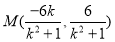 ,因为点
,因为点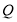 在圆上,所以
在圆上,所以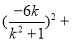
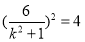 ,解得
,解得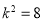 ,即
,即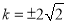 ,经验证满足条件,所以存在点
,经验证满足条件,所以存在点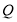 ,使得
,使得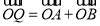 .
.
试题解析:【解析】
(Ⅰ)设圆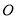 的半径为
的半径为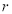 ,因为直线
,因为直线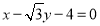 与圆
与圆 相切,
相切,
所以 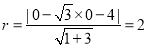 3分
3分
所以圆 的方程为
的方程为 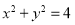 5分
5分
(Ⅱ)方法一:因为直线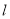 :
: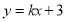 与圆
与圆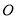 相交于
相交于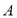 ,
,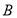 两点,
两点,
所以 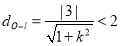 ,
,
所以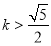 或
或 7分
7分
假设存在点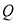 ,使得
,使得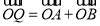 8分
8分
因为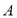 ,
,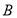 在圆上,且
在圆上,且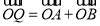 ,同时
,同时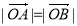
由向量加法的平行四边形法则可知
四边形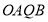 为菱形,所以
为菱形,所以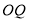 与
与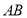 互相垂直且平分 9分
互相垂直且平分 9分
所以原点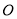 到直线
到直线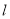 :
: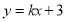 的距离为
的距离为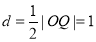 10分
10分
即 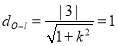 ,解得
,解得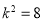 ,
, 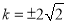 ,经验证满足条件 12分
,经验证满足条件 12分
所以存在点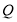 ,使得
,使得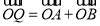 13分
13分
方法二:假设存在点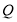 ,使得
,使得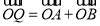 .记
.记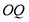 与
与 交于点
交于点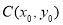
因为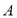 ,
,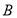 在圆上,且
在圆上,且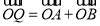 ,由向量加法的平行四边形法则可知四边形
,由向量加法的平行四边形法则可知四边形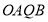 为菱形,
为菱形,
因为直线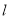 斜率为
斜率为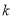 ,显然
,显然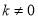 ,所以
,所以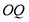 直线方程为
直线方程为 7分
7分
 , 解得
, 解得 , 所以点
, 所以点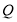 坐标为
坐标为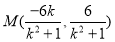 9分
9分
因为点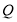 在圆上,所以
在圆上,所以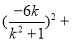
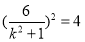 ,解得
,解得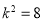 11分
11分
即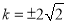 ,经验证满足条件 12分
,经验证满足条件 12分
所以存在点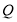 ,使得
,使得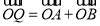 13分.
13分.
考点:1.圆的方程;2.直线与圆的位置关系.

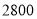 人,其中高一年级
人,其中高一年级 人,高二年级
人,高二年级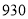 人,高三年级
人,高三年级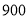 人,现采用分层抽样的方法,抽取
人,现采用分层抽样的方法,抽取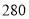 人进行体育达标检测,则抽取高二年级学生人数为 .
人进行体育达标检测,则抽取高二年级学生人数为 . 满足不等式组
满足不等式组 ,则
,则 的最小值是( ).
的最小值是( ). B.
B. C.
C. D.
D.
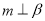 ”是“α⊥β”的充分不必要条件
”是“α⊥β”的充分不必要条件 ,若
,若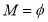 ,则实数
,则实数 的取值范围是_______________ .
的取值范围是_______________ .  表示的曲线形状是
表示的曲线形状是
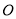 的直线
的直线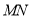 与双曲线
与双曲线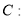
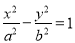 交于
交于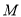 、
、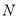 两点,
两点,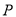 是双曲线
是双曲线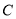 上异于
上异于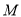 、
、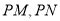 的斜率之积
的斜率之积 ,则双曲线
,则双曲线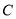 的离心率
的离心率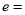
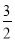 B.
B. C.
C.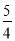 D.2
D.2

 B.
B. C.
C. D.
D.