题目内容
设α,β是空间两个平面,m, n是空间两条直线,则下列选项不正确的是( )
A.当mα时,“n∥α”是“m∥n”的必要不充分条件
B.当mα时,“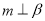 ”是“α⊥β”的充分不必要条件
”是“α⊥β”的充分不必要条件
C.当n⊥α时,“n⊥β”是“α∥β”的充要条件
D.当mα时,“n⊥α”是“m⊥n”的充分不必要条件
A
【解析】
试题分析:当mα时,如果 ,那么
,那么 ,所以
,所以 或
或 异面;反之,若
异面;反之,若 ,则
,则 或
或 ,即当mα时,“n∥α”是“m∥n”的既不必要也不充分条件,
,即当mα时,“n∥α”是“m∥n”的既不必要也不充分条件, 不正确;当mα时,如果m⊥β,则α⊥β;反之,若α⊥β,则
不正确;当mα时,如果m⊥β,则α⊥β;反之,若α⊥β,则 或
或 或
或 ,即当mα时,“
,即当mα时,“ ”是“α⊥β”的充分不必要条件,
”是“α⊥β”的充分不必要条件, 正确;当n⊥α时,若n⊥β,则α∥β;反之也成立,
正确;当n⊥α时,若n⊥β,则α∥β;反之也成立, 正确;当mα时,若 n⊥α,则
正确;当mα时,若 n⊥α,则 垂直于平面
垂直于平面 内的每一条直线,即m⊥n;反之,若m⊥n,则n⊥α不一定成立,即当mα时,“n⊥α”是“m⊥n”的充分不必要条件,
内的每一条直线,即m⊥n;反之,若m⊥n,则n⊥α不一定成立,即当mα时,“n⊥α”是“m⊥n”的充分不必要条件, 正确.选
正确.选 .
.
考点:1.充要条件;2.平行关系、垂直关系.

练习册系列答案
相关题目
 中,以直线
中,以直线 为渐近线,且经过抛物线
为渐近线,且经过抛物线 焦点的双曲线的方程是 .
焦点的双曲线的方程是 . 的解集为 .
的解集为 . 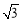 )图像上一动点,记m=
)图像上一动点,记m= , 则当m取最小值时,点P的坐标为 .
, 则当m取最小值时,点P的坐标为 . 的右焦点为F(c, 0), 方程ax2+bx-c=0的两个实根分别为x1, x2,则点P(x1, x2) ( )
的右焦点为F(c, 0), 方程ax2+bx-c=0的两个实根分别为x1, x2,则点P(x1, x2) ( ) 中,
中, 为坐标原点,以
为坐标原点,以 相切.
相切. :
: 与圆
与圆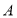 ,
, 两点,在圆
两点,在圆 ,使得
,使得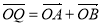 ,若存在,求出此时直线
,若存在,求出此时直线 的斜率;若不存在,说明理由.
的斜率;若不存在,说明理由.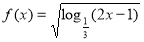 ,则
,则 的定义域为_______________ .
的定义域为_______________ . 满足约束条件
满足约束条件 ,则
,则 的最大值为_________.
的最大值为_________. 是奇函数且
是奇函数且 ,当
,当 时,
时,  (
( ),则实数
),则实数 的值为
的值为 B.
B. C.
C. D.
D.