题目内容
19.已知圆C:(x-3)2+(y-5)2=5,过圆心C的直线l交圆C于A,B两点,交y轴于点P.若A恰为PB的中点,则直线l的方程为2x-y-1=0或2x+y-11=0.分析 由题意可设直线L的方程为y-5=k(x-3),P(0,5-3k),设A(x1,y1),B(x2,y2),联立直线与圆的方程,然后由方程的根与系数关系可得,x1+x2,x1x2,由A为PB的中点可得x2=2x1,联立可求x1,x2,进而可求k,即可求解直线方程.
解答 解:由题意可得,C(3,5),直线L的斜率存在
可设直线L的方程为y-5=k(x-3)
令x=0可得y=5-3k,即P(0,5-3k),设A(x1,y1),B(x2,y2)
联立直线与圆的方程,消去y可得(1+k2)x2-6(1+k2)x+9k2+4=0
由方程的根与系数关系可得,x1+x2=6,x1x2=$\frac{9{k}^{2}+4}{1+{k}^{2}}$①
∵A为PB的中点
∴x2=2x1②
把②代入①可得x2=4,x1=2,x1x2=$\frac{9{k}^{2}+4}{1+{k}^{2}}$=8
∴k=±2
∴直线l的方程为y-5=±2(x-3),即2x-y-1=0或2x+y-11=0.
故答案为:2x-y-1=0或2x+y-11=0.
点评 本题主要考查直线和圆的位置关系,方程的根与系数关系的应用,体现了方程思想,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
4.下列求导数运算正确的是( )
| A. | ${(x+\frac{1}{x})^'}=1+\frac{1}{x^2}$ | B. | (lgx)′=$\frac{1}{xlge}$ | C. | (3x)′=3xln3 | D. | (x2cosx)′=-2xsinx |
9.若集合A={-2,-1,0,1,2},B={x||x|≤1},则A∩B=( )
| A. | {-1,0,1} | B. | {0,1} | C. | {x|-1≤x≤1} | D. | {x|0≤x≤1} |
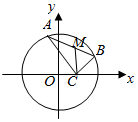 已知点C(1,0),点A,B是⊙O:x2+y2=9上任意两个不同的点,且满足$\overrightarrow{AC}$•$\overrightarrow{BC}$=0,设M为弦AB的中点.
已知点C(1,0),点A,B是⊙O:x2+y2=9上任意两个不同的点,且满足$\overrightarrow{AC}$•$\overrightarrow{BC}$=0,设M为弦AB的中点.