题目内容
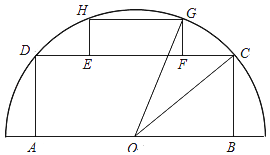
【题目】如图,在半径为2的扇形AOB中,∠AOB=90°,P为 ![]() 上的一点,若
上的一点,若 ![]() =2,则
=2,则 ![]() 的值为 .
的值为 . 
【答案】2 ![]() ﹣2
﹣2
【解析】解:如图,连接BP,AP,设OP交AB于点M,
∵半径为2, ![]() =|
=| ![]() ||
|| ![]() |cos∠AOP=2×2×cos∠AOP=2,解得cos∠AOP=
|cos∠AOP=2×2×cos∠AOP=2,解得cos∠AOP= ![]() ,可得∠AOP=60°,
,可得∠AOP=60°,
∴由∠AOB=90°,可得:∠POB=30°,可得:∠BPO=∠PBO=75°,
又∵∠ABO=∠BAO=45°,可得:∠PBA=∠PBO﹣∠ABO=75°﹣45°=30°,
∴∠PMB=180°﹣∠OPB﹣∠PBA=180°﹣75°﹣30°=75°,
∴ ![]() =|
=| ![]() ||
|| ![]() |cos∠PMB=2×
|cos∠PMB=2× ![]() ×cos75°=4
×cos75°=4 ![]() ×cos(45°+30°)=4
×cos(45°+30°)=4 ![]() ×
× ![]() =2
=2 ![]() ﹣2.
﹣2.
所以答案是:2 ![]() ﹣2.
﹣2.

【考点精析】解答此题的关键在于理解扇形面积公式的相关知识,掌握若扇形的圆心角为![]() ,半径为
,半径为![]() ,弧长为
,弧长为![]() ,周长为
,周长为![]() ,面积为
,面积为![]() ,则
,则![]() ,
,![]() ,
,![]() .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目