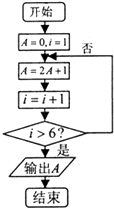
题目内容
【题目】在平面直角坐标系xOy中,椭圆E: ![]() =1(a>b>0)的离心率为
=1(a>b>0)的离心率为 ![]() ,右焦点为F,且椭圆E上的点到点F的距离的最小值为2.
,右焦点为F,且椭圆E上的点到点F的距离的最小值为2.
(1)求a,b的值;
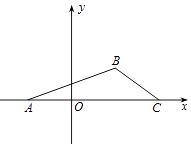
(2)设椭圆E的左、右顶点分别为A,B,过点A的直线l与椭圆E及直线x=8分别相交于点M,N
①当过点A,F,N三点的圆半径最小时,求这个圆的方程;②若cos∠AMB= ![]() ,求△ABM的面积.
,求△ABM的面积.
【答案】
(1)解:由已知, ![]() =
= ![]() ,且a﹣c=2,
,且a﹣c=2,
解得a=4,c=2,
∴b2=a2﹣c2=12,
∴a=4,b=2 ![]() ;
;
(2)①由(1),A(﹣4,0),F(2,0),设N(8,t).
再设圆的方程为x2+y2+Dx+Ey+F=0,将点A,F,N的坐标代入,
得 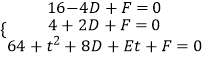 ,解得
,解得 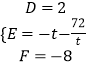 ,
,
∴圆的方程为x2+y2+2x﹣(t+ ![]() )y﹣8=0,
)y﹣8=0,
即(x+1)2+[y﹣ ![]() (t+
(t+ ![]() )]2=9+
)]2=9+ ![]() (t+
(t+ ![]() )2,
)2,
∵(t+ ![]() )2≥(2
)2≥(2 ![]() )2,当且仅当t+
)2,当且仅当t+ ![]() =±12
=±12 ![]() 时,圆的半径最小,
时,圆的半径最小,
故所求圆的方程为x2+y2+2x±12 ![]() y﹣8=0.
y﹣8=0.
②由对称性不妨设直线l的方程为y=k(x+4)(k>0).
由  ,得M(
,得M( ![]() ,
, ![]() ),
),
∴ ![]() =(
=( ![]() ,
, ![]() ),
), ![]() =(
=( ![]() ,
, ![]() ),
),
∴cos∠AMB= 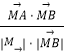 =
= ![]() =﹣
=﹣ ![]() ,
,
化简,得16k4﹣40k2﹣9=0,
解得k2= ![]() ,或k2=
,或k2= ![]() ,即k=
,即k= ![]() ,或k=
,或k= ![]() ,
,
此时总有yM=3.
∴△ABM的面积为 ![]() ×8×3=12.
×8×3=12.
【解析】1、本题考查的是由待定系数法求椭圆的方程。
2、(1)由已知条件,A(﹣4,0),F(2,0),设N(8,t).再设圆的方程为x2+y2+Dx+Ey+F=0,将点A,F,N的坐标代入得到圆的一般方程![]() ,把圆的方程整理基本不等式的形式求出最小值,当且仅当
,把圆的方程整理基本不等式的形式求出最小值,当且仅当![]() 圆的半径最小,故所求圆的方程为x2+y2+2x±12 2 y﹣8=0. (2)由对称性不妨设直线l的方程为y=k(x+4)(k>0)可得向量MA和MB的坐标表示,再由cos∠AMB的公式求得k的值,点M到直线的距离为3,所以三角形的面积为12.
圆的半径最小,故所求圆的方程为x2+y2+2x±12 2 y﹣8=0. (2)由对称性不妨设直线l的方程为y=k(x+4)(k>0)可得向量MA和MB的坐标表示,再由cos∠AMB的公式求得k的值,点M到直线的距离为3,所以三角形的面积为12.

 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案【题目】某花店每天以每枝5元的价格从农场购进若干枝玫瑰花,然后以每枝10元的价格出售,如果当天卖不完,剩下的玫瑰花作垃圾处理.
(1)若花店一天购进16枝玫瑰花,求当天的利润y(单位:元)关于当天需求量n(单位:枝,n∈N)的函数解析式.
(2)花店记录了100天玫瑰花的日需求量(单位:枝),整理得如表:
日需求量n | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
频数 | 10 | 20 | 16 | 16 | 15 | 13 | 10 |
以100天记录的各需求量的频率作为各需求量发生的概率.
(i)若花店一天购进16枝玫瑰花,X表示当天的利润(单位:元),求X的分布列,数学期望及方差;
(ii)若花店计划一天购进16枝或17枝玫瑰花,你认为应购进16枝还是17枝?请说明理由.