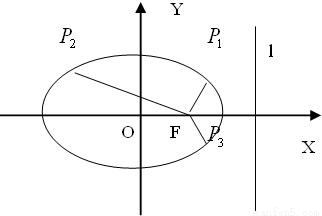
题目内容
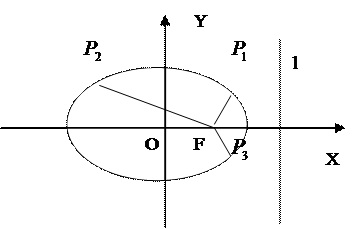
中心在原点O的椭圆的左焦点为F(-1,0),上顶点为(0, ),P1、P2、P3是椭圆上任意三个不同点,且∠P1FP2=∠P2FP3=∠P3FP1,则
),P1、P2、P3是椭圆上任意三个不同点,且∠P1FP2=∠P2FP3=∠P3FP1,则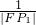 +
+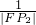 +
+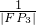 =
=
- A.2
- B.3
- C.1
- D.-1
A
分析:设椭圆方程为 ,由题意知c=1,
,由题意知c=1, ,a=2故所求椭圆方程为
,a=2故所求椭圆方程为  .
.
记椭圆的右顶点为A,并设∠AFPi=αi(i=1,2,3),假设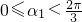 ,且
,且 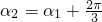 ,
,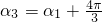
又设点Pi在l上的射影为Qi,因椭圆的离心率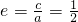 ,从而有|FPi|=|PiQi|•e=
,从而有|FPi|=|PiQi|•e=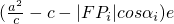 =
=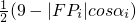 (i=1,2,3).由此入手能够推导出
(i=1,2,3).由此入手能够推导出 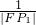 +
+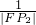 +
+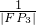 为定值,并能求出此定值.
为定值,并能求出此定值.
解答: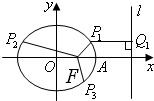 解:设椭圆方程为
解:设椭圆方程为  ,由题意知c=1,
,由题意知c=1, ,a=2故所求椭圆方程为
,a=2故所求椭圆方程为  .
.
记椭圆的右顶点为A,并设∠AFPi=αi(i=1,2,3),不失一般性,
假设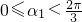 ,且
,且 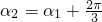 ,
,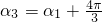
又设点Pi在l上的射影为Qi,因椭圆的离心率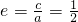 ,从而有|FPi|=|PiQi|•e=
,从而有|FPi|=|PiQi|•e=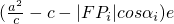 =
=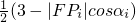 (i=1,2,3)
(i=1,2,3)
解得 =
=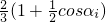 (i=1,2,3)
(i=1,2,3)
因此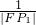 +
+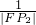 +
+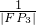 =
=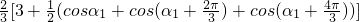 ,
,
而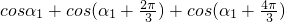 =
=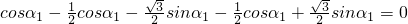 ,
,
故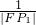 +
+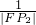 +
+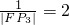 .
.
故选A.
点评:本题考查直线和椭圆的位置关系和综合运用,解题时要认真审题,仔细解答,注意挖掘题中的隐含条件.
分析:设椭圆方程为
 ,由题意知c=1,
,由题意知c=1, ,a=2故所求椭圆方程为
,a=2故所求椭圆方程为  .
.记椭圆的右顶点为A,并设∠AFPi=αi(i=1,2,3),假设
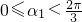 ,且
,且 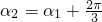 ,
,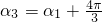
又设点Pi在l上的射影为Qi,因椭圆的离心率
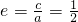 ,从而有|FPi|=|PiQi|•e=
,从而有|FPi|=|PiQi|•e=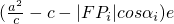 =
=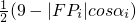 (i=1,2,3).由此入手能够推导出
(i=1,2,3).由此入手能够推导出 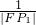 +
+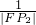 +
+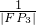 为定值,并能求出此定值.
为定值,并能求出此定值.解答:
 解:设椭圆方程为
解:设椭圆方程为  ,由题意知c=1,
,由题意知c=1, ,a=2故所求椭圆方程为
,a=2故所求椭圆方程为  .
.记椭圆的右顶点为A,并设∠AFPi=αi(i=1,2,3),不失一般性,
假设
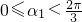 ,且
,且 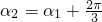 ,
,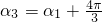
又设点Pi在l上的射影为Qi,因椭圆的离心率
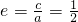 ,从而有|FPi|=|PiQi|•e=
,从而有|FPi|=|PiQi|•e=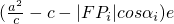 =
=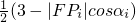 (i=1,2,3)
(i=1,2,3)解得
 =
=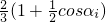 (i=1,2,3)
(i=1,2,3)因此
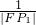 +
+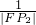 +
+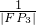 =
=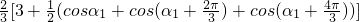 ,
,而
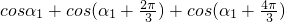 =
=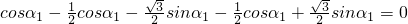 ,
,故
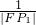 +
+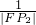 +
+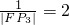 .
.故选A.
点评:本题考查直线和椭圆的位置关系和综合运用,解题时要认真审题,仔细解答,注意挖掘题中的隐含条件.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
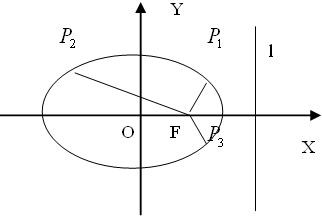 如图,中心在原点O的椭圆的右焦点为F(3,0),右准线l的方程为:x=12.
如图,中心在原点O的椭圆的右焦点为F(3,0),右准线l的方程为:x=12.
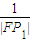 +
+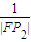 +
+ 为定值,并求此定值.
为定值,并求此定值.