Question

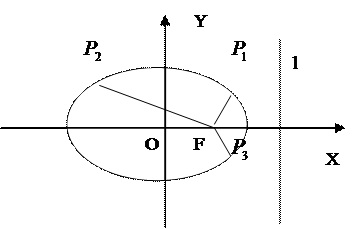
(本小题满分12分)如图，中心在原点O的椭圆的右焦点为F（3，0），

右准线l的方程为：x = 12。

（1）求椭圆的方程；

（2）在椭圆上任取三个不同点，使，

证明:  为定值，并求此定值。

 

Answer 1

解：（I）设椭圆方程为．

因焦点为，故半焦距．

又右准线的方程为，从而由已知

，

因此，．

故所求椭圆方程为．

（II）记椭圆的右顶点为，并设（1，2，3），不失一般性，

假设，且，．

又设点在上的射影为，因椭圆的离心率，从而有

  ．

解得 ．

因此

，

而

，

故为定值．

解析:

解：（I）设椭圆方程为．

因焦点为，故半焦距．

又右准线的方程为，从而由已知

，

因此，．

故所求椭圆方程为．

（II）记椭圆的右顶点为，并设（1，2，3），不失一般性，

假设，且，．

又设点在上的射影为，因椭圆的离心率，从而有

  ．

解得 ．

因此

，

而

，

故为定值．