题目内容
设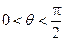 ,曲线
,曲线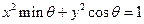 和
和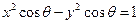 有4个不同的交点.
有4个不同的交点.
(1)求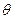 的取值范围;
的取值范围;
(2)证明这4个次点共圆,并求圆半径的取值范围.
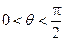 ,曲线
,曲线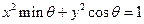 和
和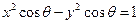 有4个不同的交点.
有4个不同的交点.(1)求
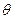 的取值范围;
的取值范围;(2)证明这4个次点共圆,并求圆半径的取值范围.
(1)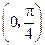 (2)
(2)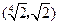
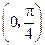 (2)
(2)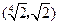
(1)两曲线的交点坐标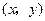 满足方程组
满足方程组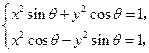 即
即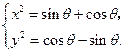
有4个不同交点等价于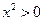 且
且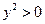 ,即
,即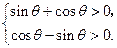
又因为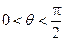 ,所以得
,所以得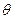 的取值范围为
的取值范围为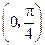 .
.
(2)由(1)推理知4个交点的坐标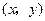 满足方程
满足方程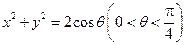 ,即得4个交点共圆,该圆的圆心在原点,半径为
,即得4个交点共圆,该圆的圆心在原点,半径为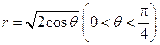 .
.
因为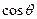 在
在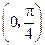 上是减函数,所以由
上是减函数,所以由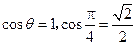 .
.
知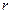 的取值范围是
的取值范围是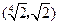 .
.
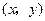 满足方程组
满足方程组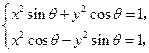 即
即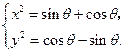
有4个不同交点等价于
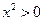 且
且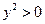 ,即
,即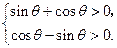
又因为
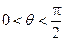 ,所以得
,所以得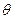 的取值范围为
的取值范围为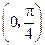 .
.(2)由(1)推理知4个交点的坐标
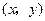 满足方程
满足方程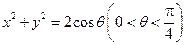 ,即得4个交点共圆,该圆的圆心在原点,半径为
,即得4个交点共圆,该圆的圆心在原点,半径为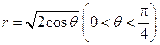 .
.因为
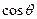 在
在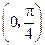 上是减函数,所以由
上是减函数,所以由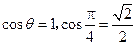 .
.知
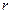 的取值范围是
的取值范围是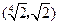 .
.
练习册系列答案
 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案
相关题目
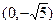 是中心在原点,长轴在x轴上的椭圆的一个顶点,离心率为
是中心在原点,长轴在x轴上的椭圆的一个顶点,离心率为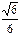 ,椭圆的左右焦点分别为F1和F2 。
,椭圆的左右焦点分别为F1和F2 。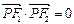 ,若存在,请求出点P的坐标;若不存在,请说明理由。
,若存在,请求出点P的坐标;若不存在,请说明理由。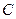 上任意一点
上任意一点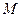 到点
到点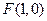 的距离比它到直线
的距离比它到直线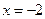 的距离小1.
的距离小1.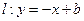 与曲线
与曲线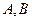 两点,
两点,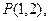 设直线
设直线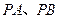 的斜率分别为
的斜率分别为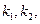
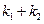 为定值.
为定值.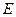 的中心在原点,焦点在
的中心在原点,焦点在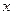 轴上,椭圆上的点到焦点的距离的最小值为
轴上,椭圆上的点到焦点的距离的最小值为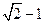 ,离心率为
,离心率为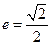 .
.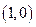 作直线
作直线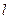 交
交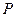 、
、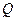 两点,试问:在
两点,试问:在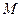 ,使
,使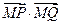 为定值?若存在,求出这个定点
为定值?若存在,求出这个定点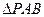 所在的平面
所在的平面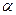 和四边形
和四边形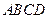 所在的平面
所在的平面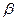 垂直,且
垂直,且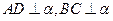 ,
,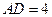 ,
,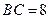 ,
,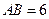 ,
,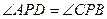 ,则点
,则点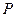 在平面
在平面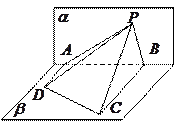
 ,
, 距离相等的点的坐标
距离相等的点的坐标 满足的条件.
满足的条件.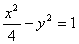 , 直线
, 直线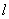 通过其右焦点F2,且与双曲线的右支交于A、B两点,将A、B与双曲线的左焦点F1连结起来,求|F1A|·|F1B|的最小值
通过其右焦点F2,且与双曲线的右支交于A、B两点,将A、B与双曲线的左焦点F1连结起来,求|F1A|·|F1B|的最小值
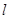 的参数方程为
的参数方程为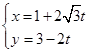 (
(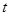 为参数),则直线
为参数),则直线


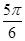
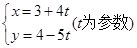 的斜率为______________________。
的斜率为______________________。