题目内容
已知双曲线的方程为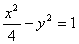 , 直线
, 直线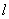 通过其右焦点F2,且与双曲线的右支交于A、B两点,将A、B与双曲线的左焦点F1连结起来,求|F1A|·|F1B|的最小值
通过其右焦点F2,且与双曲线的右支交于A、B两点,将A、B与双曲线的左焦点F1连结起来,求|F1A|·|F1B|的最小值
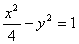 , 直线
, 直线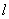 通过其右焦点F2,且与双曲线的右支交于A、B两点,将A、B与双曲线的左焦点F1连结起来,求|F1A|·|F1B|的最小值
通过其右焦点F2,且与双曲线的右支交于A、B两点,将A、B与双曲线的左焦点F1连结起来,求|F1A|·|F1B|的最小值
设A(x1,y1),B(x2,y2),A到双曲线的左准线x= ─ = ─
= ─ 的距离
的距离
d=|x1+ |=x1+
|=x1+ ,由双曲线的定义,
,由双曲线的定义, =e=
=e= ,∴|AF1|=
,∴|AF1|= (x1+
(x1+ )=
)= x1+2,
x1+2,
同理,|BF1|= x2+2,∴|F1A|·|F1B|=(
x2+2,∴|F1A|·|F1B|=( x1+2)(
x1+2)( x2+2)=
x2+2)= x1x2+
x1x2+ (x1+x2)+4 (1)
(x1+x2)+4 (1)
双曲线的右焦点为F2( ,0),
,0),
(1)当直线的斜率存在时设直线AB的方程为:y=k(x─ ),
),
由 消去y得 (1─4k2)x2+8
消去y得 (1─4k2)x2+8 k2x─20k2─4=0,
k2x─20k2─4=0,
∴x1+x2= , x1x2= ─
, x1x2= ─ , 代入(1)整理得
, 代入(1)整理得
|F1A|·|F1B|= +4=
+4= +4=
+4= +4=
+4= +
+
∴|F1A|·|F1B|> ;
;
(2)当直线AB垂直于x轴时,容易算出|AF2|=|BF2|= ,
,
∴|AF1|=|BF1|=2a+ =
= (双曲线的第一定义), ∴|F1A|·|F1B|=
(双曲线的第一定义), ∴|F1A|·|F1B|=
由(1), (2)得:当直线AB垂直于x轴时|F1A|·|F1B| 取最大值

 = ─
= ─ 的距离
的距离d=|x1+
 |=x1+
|=x1+ ,由双曲线的定义,
,由双曲线的定义, =e=
=e= ,∴|AF1|=
,∴|AF1|= (x1+
(x1+ )=
)= x1+2,
x1+2,同理,|BF1|=
 x2+2,∴|F1A|·|F1B|=(
x2+2,∴|F1A|·|F1B|=( x1+2)(
x1+2)( x2+2)=
x2+2)= x1x2+
x1x2+ (x1+x2)+4 (1)
(x1+x2)+4 (1)双曲线的右焦点为F2(
 ,0),
,0), (1)当直线的斜率存在时设直线AB的方程为:y=k(x─
 ),
),由
 消去y得 (1─4k2)x2+8
消去y得 (1─4k2)x2+8 k2x─20k2─4=0,
k2x─20k2─4=0,∴x1+x2=
 , x1x2= ─
, x1x2= ─ , 代入(1)整理得
, 代入(1)整理得|F1A|·|F1B|=
 +4=
+4= +4=
+4= +4=
+4= +
+
∴|F1A|·|F1B|>
 ;
;(2)当直线AB垂直于x轴时,容易算出|AF2|=|BF2|=
 ,
,∴|AF1|=|BF1|=2a+
 =
= (双曲线的第一定义), ∴|F1A|·|F1B|=
(双曲线的第一定义), ∴|F1A|·|F1B|=
由(1), (2)得:当直线AB垂直于x轴时|F1A|·|F1B| 取最大值


点拨与提示:由双曲线的定义得:|AF1|= (x1+
(x1+ )=
)= x1+2,|BF1|=
x1+2,|BF1|= x2+2,
x2+2,
|F1A|·|F1B|=( x1+2)(
x1+2)( x2+2)=
x2+2)= x1x2+
x1x2+ (x1+x2)+4 ,将直线方程和双曲线的方程联立消元,得x1+x2=
(x1+x2)+4 ,将直线方程和双曲线的方程联立消元,得x1+x2= , x1x2= ─
, x1x2= ─ .本题要注意斜率不存在的情况.
.本题要注意斜率不存在的情况.
 (x1+
(x1+ )=
)= x1+2,|BF1|=
x1+2,|BF1|= x2+2,
x2+2,|F1A|·|F1B|=(
 x1+2)(
x1+2)( x2+2)=
x2+2)= x1x2+
x1x2+ (x1+x2)+4 ,将直线方程和双曲线的方程联立消元,得x1+x2=
(x1+x2)+4 ,将直线方程和双曲线的方程联立消元,得x1+x2= , x1x2= ─
, x1x2= ─ .本题要注意斜率不存在的情况.
.本题要注意斜率不存在的情况.
练习册系列答案
相关题目




 面积的最小值。
面积的最小值。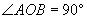 ,内有一动点P,
,内有一动点P,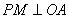 于M,
于M,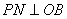 于N,且四边形PMON的面积等于4,今以O为原点,
于N,且四边形PMON的面积等于4,今以O为原点,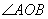 的平分线
的平分线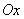 为极轴(如图),求动点P的轨迹方程。
为极轴(如图),求动点P的轨迹方程。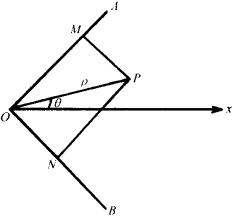
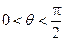 ,曲线
,曲线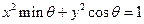 和
和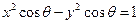 有4个不同的交点.
有4个不同的交点.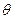 的取值范围;
的取值范围; 如图,已知圆O:x2+y2=2交x轴于A,B两点,曲线C是以AB为长轴,离心率为
如图,已知圆O:x2+y2=2交x轴于A,B两点,曲线C是以AB为长轴,离心率为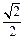 的椭圆,其右焦点为F.若点P(-1,1)为圆O上一点,连结PF,过原点O作直线PF的垂线交椭圆C的右准线l于点Q.(1)求椭圆C的标准方程;
的椭圆,其右焦点为F.若点P(-1,1)为圆O上一点,连结PF,过原点O作直线PF的垂线交椭圆C的右准线l于点Q.(1)求椭圆C的标准方程;



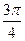 ,直线
,直线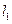 经过点A(3,2),B(a,-1),且
经过点A(3,2),B(a,-1),且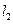 :2x+by+1=0与直线
:2x+by+1=0与直线